Prova Unicamp 2020

Olá, pessoal… Tudo bem? Sou a prof. Marçal, do Estratégia Vestibulares, e escrevo este artigo para lançar o Gabarito UNICAMP 2020, da disciplina de Matemática. Nesta página, você vai conferir a resolução comentada completa. Vamos nessa??

">Prova UNICAMP 2020 – Matemática – Correção" class="wp-block-file__button" download>Baixar

Questão 80

“(…) as palavras tomam significados distintos daqueles utilizados no cotidiano. Por exemplo, utiliza-se, com frequência, nas aulas sobre frações, a frase reduzir ao mesmo denominador.”

(Edi Jussara Cândido Lorensatti, Linguagem matemática e Língua Portuguesa: diálogo

necessário na resolução de problemas matemáticos. Conjectura: Filosofia e Educação

Caxias do Sul, v. 14, n. 2, p. 91, maio/ago. 2009.)

Cada ciência usa uma linguagem própria e com um grau de precisão terminológica necessário para o seu exercício. Tendo em vista os significados distintos que as palavras assumem nas situações concretas em que são empregadas, o verbo “reduzir”, no uso cotidiano, significa

a) limitar alguma coisa, ao passo que na linguagem matemática é sinônimo de restringir.

b) moderar alguma coisa, ao passo que na linguagem matemática implica aumentar as relações entre os números.

c) eliminar alguma coisa, ao passo que na linguagem matemática implica reverter as relações entre os números.

d) diminuir alguma coisa, ao passo que na linguagem matemática é sinônimo de converter.

Resolução Comentada

No cotidiano, reduzir significa diminuir. No contexto matemático das frações, pode ser entendido com reescrever uma fração, ou seja, convertê-la em outro formato.

Gabarito: d)

Questão 32

Em uma família, cada filha tem o mesmo número de irmãs e irmãos, e cada filho tem um número de irmãs igual ao dobro do número de irmãos. O número total de filhos e filhas dessa família é igual a

a) 11.

b) 9.

c) 7.

d) 5.

Resolução Comentada

Para uma filha, podemos dizer que o número de irmãs, sendo $\dpi{100} \large A$ o número de filhas, é dado por $\dpi{100} \large A-1$ , pois uma filha não é considerada irmã de si mesma. Já o número de irmãos de uma filha, sendo O o número de filhos, é dado por O mesmo.

Já para um filho, o número de irmãos é igual a $\dpi{100} \large O-1$ pelo mesmo motivo citado anteriormente. O número de irmãs de um filho é igual a $\dpi{100} \large A$ .

Dessa forma, pelo enunciado, podemos montar o seguinte sistema de equações:

$\dpi{100} \left\{\begin{matrix}A-1=O\\\ \\2\cdot\left(O-1\right)=A\\\end{matrix}\right.\rightarrow\left\{\begin{matrix}A-1=O\\\ \\2\cdot O-2=A\\\end{matrix}\right.\rightarrow$

$\dpi{100} \left\{\begin{matrix}A-O=1\\\ \\-A+2\cdot O=2\\\end{matrix}\right.\rightarrow\left\{\begin{matrix}A-O=1\\\ \\O=3\\\end{matrix}\right.\rightarrow\left\{\begin{matrix}A=4\\\ \\O=3\\\end{matrix}\right.$

De posse do número de filhos O e de filhas A, a soma é dada por:

$\dpi{100} A+O=4+3=7$

Gabarito: C

Questão 33

Cinco pessoas devem ficar em pé, uma ao lado da outra, para tirar uma fotografia, sendo que duas delas se recusam a ficar lado a lado. O número de posições distintas para as cinco pessoas serem fotografadas juntas é igual a

a) 48.

b) 72.

c) 96.

d) 120.

Resolução Comentada

Se não houvesse restrição, o número de maneiras de colocarmos cinco pessoas em linha é dado por:

$\dpi{100} \large P_5=5!=5\cdot 4\cdot 3\cdot 2\cdot 1$

Considerando as duas pessoas “enguiçadas” como uma só (modo proibido), temos:

$\dpi{100} \large 2\cdot P_4=2\cdot 4\cdot 3\cdot 2\cdot 1$

Dessa maneira, o número de modos permitidos para enfileirarmos essas pessoas, de modo que as duas que se recusam a ficar lado a lado não sejam contrariadas, é dado pela diferença:

$\dpi{100} \large 5\cdot4\cdot3\cdot2\cdot1-2\cdot4\cdot3\cdot2\cdot1$

$\dpi{100} \large 3\cdot4\cdot3\cdot2\cdot1\\$

$\dpi{100} \large 72$

Gabarito: B

Questão 34

Um atleta participa de um torneio composto por três provas. Em cada prova, a probabilidade de ele ganhar é de 2/3, independentemente do resultado das outras provas.

Para vencer o torneio, é preciso ganhar pelo menos duas provas. A probabilidade de o atleta vencer o torneio é igual a

a) 2/3.

b) 4/9.

c) 20/27.

d) 16/81.

Resolução Comentada

Considerando V a situação em que o atleta vence e P a situação em que o atleta perde uma prova, temos que, para vender o torneio, deverá ocorrer uma das seguintes situações:

$\dpi{100} \large VVV$

$\dpi{100} \large VVP$

$\dpi{100} \large VPV$

$\dpi{100} \large PVV$

Como as situações agrupadas são alternativas, ou seja, deve ocorrer uma OU outra, a probabilidade é dada pela soma:

$\dpi{100} \large \frac{2}{3}\cdot\frac{2}{3}\cdot\frac{2}{3}+\frac{2}{3}\cdot\frac{2}{3}\cdot\frac{1}{3}+\frac{2}{3}\cdot\frac{1}{3}\cdot\frac{2}{3}+\frac{1}{3}\cdot\frac{2}{3}\cdot\frac{2}{3}$

$\dpi{100} \large \frac{8}{27}+3\cdot\frac{4}{27}$

$\dpi{100} \large \frac{20}{27}$

Gabarito: C

Questão 35

Sabendo que $\dpi{100} \large a$ é um número real, considere a função $\dpi{100} \large f\left(x\right)=ax+2$ , definida para todo número real $\dpi{100} \large x$ . Se $\dpi{100} \large f\left(f\left(1\right)\right)=1$ , então:

a) $\dpi{100} \large a=-1$

b) $\dpi{100} \large a=-\frac{1}{2}$

c) $\dpi{100} \large a=\frac{1}{2}$

d) $\dpi{100} \large a=1$

Resolução Comentada

Como a questão pediu uma função composta envolvendo $\dpi{100} \large f(1)$ , vamos adiantar nosso trabalho e calcular $\dpi{100} \large f(1)$ .

$\dpi{100} \large f\left(x\right)=ax+2$

$\dpi{100} \large f\left(1\right)=a\cdot1+2$

$\dpi{100} \large f\left(1\right)=a+2$

Se posse de $\dpi{100} \large f(1)$ , vamos substitui-la na equação $\dpi{100} \large f\left(f\left(1\right)\right)=1$ dada no enunciado.

$\dpi{100} \large f\left(x\right)=ax+2$

$\dpi{100} \large f\left(f\left(1\right)\right)=a\cdot f\left(1\right)+2$

$\dpi{100} \large 1=a\cdot(a+2)+2$

$\dpi{100} \large 1=a^2+2a+2$

$\dpi{100} \large 0=a^2+2a+1$

$\dpi{100} \large 0=\left(a+1\right)^2$

$\dpi{100} \large a=-1$

Gabarito: A

Questão 36

Sabendo que $\dpi{100} \large a$ é um número real, considere a equação quadrática $\dpi{100} \large 2x^2+ax+10=0$ . Se as soluções dessa equação são números inteiros, o módulo da soma das soluções é igual a

a) 3.

b) 4.

c) 5.

d) 6.

Resolução Comentada

Dada a equação

$\dpi{100} \large 2x^2+ax+10=0$

Temos, pelas relações de Girard:

$\dpi{100} \large \left\{\begin{matrix}x^\prime+x^{\prime\prime}=-\frac{a}{2}\\\ \\x^\prime\cdot x^{\prime\prime}=\frac{10}{2}=5\\\end{matrix}\right.$

Para que o produto de dois números inteiros, x” e x”,seja igual a 5, temos apenas duas opções:

$\dpi{100} \large \left\{\begin{matrix}x^\prime=1\\\ \\x^{\prime\prime}=5\\\end{matrix}\right.$

$\dpi{100} \large \left\{\begin{matrix}x^\prime=-1\\\ \\x^{\prime\prime}=-5\\\end{matrix}\right.$

De todo modo, temos:

$\dpi{100} \large \left|x^\prime+x^{\prime\prime}\right|=6$

Gabarito: D

Questão 37

Considere que (a, b, 3, c) é uma progressão aritmética de números reais, e que a soma de seus elementos é igual a 8. O produto dos elementos dessa progressão é igual a

a) 30.

b) 10.

c) -15.

d) -20.

Resolução Comentada

Para reduzir o número de incógnitas, vamos reescrever a progressão com base na razão r.

$\dpi{100} \large (a,b,3,c)$

$\dpi{100} \large (3-2r,3-r,3,3+r)$

O enunciado informou que a soma dos elementos da progressão é igual a 8, então, vamos escrever e resolver essa equação.

$\large 3-2r+3-r+3+3+r=8$

$\large 12-2r=8$

$\large 4=2r$

$\large 2=r$

De posse da razão, podemos estabelecer quais são os elementos da progressão:

$\large (3-2r,3-r,3,3+r)$

$\large (3-2\cdot2,3-2,3,3+2)$

$\large (-1,1,3,5)$

Como nossa questão pede o produto dos elementos, temos:

$\large \left(-1\right)\cdot\left(1\right)\cdot\left(3\right)\cdot\left(5\right)=-15$

Gabarito: C

Questão 38

Tendo em vista que $\large a$ e $\large b$ são números reais positivos, $\large a\neq b$ , considere a função $\large f\left(x\right)=ab^x$ , definida para todo número real $\large x$ . Logo, $\large f(2)$ é igual a:

a) $\large \sqrt{f\left(1\right)f(3)}$

b) $\large f(3)/f(2)$

c) $\large f\left(0\right)f(1)$

d) $\large f\left(0\right)^3$

Resolução Comentada

O exercício não dá uma direção específica no enunciado, então, é interessante olhar para as alternativas para entender qual é o tipo de resposta esperada.

Ao perceber que todas apresentam $\large f(x)$ para $\large x=0,1,2,3$ ; vamos começar por calcular esses valores.

$\large f(0)=a$

$\large f(1)=ab$

$\large f(2)=ab^{2}$

$\large f(3)=ab^{3}$

Perceba que $\large f(3)$ pode ser reescrito em função de $\large f(2)$ .

Muito bem, falta o termo b. Podemos reescrever a equação acima como:

$\large f(3)=f(2)\cdot\frac{f(2)}{f(1)}$

Como a questão pede a expressão equivalente a $\large f(2)$ , temos:

$\large f(3)=\frac{\left[f\left(2\right)\right]^2}{f(1)}$

$\large f\left(3\right)\cdot f(1)=\left[f\left(2\right)\right]^2$

$\large \sqrt{f\left(3\right)\cdot f(1)}=f\left(2\right)$

Gabarito: A

Questão 39

Sabendo que $\large p$ é um número real, considere a matriz

$\large A=\left[\begin{matrix}p&2\\0&p\\\end{matrix}\right]$

e sua transposta $\large A^{T}$ . Se $\large A+A^T$ singular (não invertível), então:

a) $\large p=0$

b) $\large \left | p \right |=1$

c) $\large \left | p \right |=2$

d) $\large p=3$

Resolução Comentada

O enunciado nos informa que $\large A+A^T$ é singular. Então, vamos calcular $\large A+A^T$ .

$\large A=\left[\begin{matrix}p&2\\0&p\\\end{matrix}\right]$

$\large A^T=\left[\begin{matrix}p&0\\2&p\\\end{matrix}\right]$

$\large A+A^T=\left[\begin{matrix}p&2\\0&p\\\end{matrix}\right]+\left[\begin{matrix}p&0\\2&p\\\end{matrix}\right]$

$\large A+A^T=\left[\begin{matrix}2p&2\\2&2p\\\end{matrix}\right]$

Como $\large \left(A+A^T\right)$ é singular, temos que seu determinante é nulo.

$\large \det{\left(A+A^T\right)}=0$

$\large \left|\begin{matrix}2p&2\\2&2p\\\end{matrix}\right|=0$

$\large 4p^2-4=0$

$\large 4p^2=4$

$\large p^2=1$

$\large \sqrt{p^2}=\sqrt1$

$\large \left|p\right|=1$

Gabarito: B

Questão 40

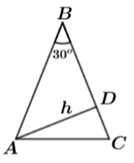
A figura abaixo exibe o triângulo $\large ABC$ , em que $\large AB=BC$ e $\large AD$ é uma altura de comprimento $\large h$ . A área do triângulo $\large ABC$ é igual a

a) $\large h^{2}$

b) $\large \sqrt2h^2$

c) $\large \sqrt3h^2$

d) $\large 2h^{2}$

Resolução Comentada

Percebendo que o triângulo $\large ADB$ é um retângulo em $\large D$ , temos:

$\large sen(30\degree)=\frac{h}{AB}$

$\large \frac{1}{2}=\frac{h}{AB}$

$\large AB=2h$

Bem, a área do triângulo $\large ABC$ pode ser escrita em função do lado $\large BC$ e da altura $\large h$ :

$\large Area=\frac{1}{2}\cdot BC\cdot h$

$\large Area=\frac{1}{2}\cdot AB\cdot h$

$\large Area=\frac{1}{2}\cdot 2h\cdot h$

$\large Area=h^{2}$

Gabarito: A

Questão 41

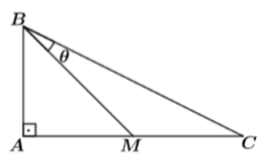
A figura abaixo exibe o triângulo retângulo $\large ABC$ , em que $\large AB=AM=MC$ . Então, $\large tg\theta$ é igual a

a) 1/2

b) 1/3

c) 1/4

d) 1/5

Resolução Comentada

Como $\large AB=AM$ e o triângulo $\large ABM$ é retângulo em $\large A$ , temos que $\large A\widehat{B}M=A\widehat{M}B=45\degree$ . Dessa forma, $\large A\widehat{B}M=45\degree+\theta$ .

O triângulo $\large ABC$ é retângulo em $\large A$ e, pelo enunciado, $\large AC=2AM$ .

Dessa forma, podemos dizer que:

$\large tg(\theta + 45\degree) = \frac{2a}{a}$

$\large \frac{tg(\theta )+tg(45\degree)}{1-tg(\theta )\cdot tg(45\degree)}=2$

$\large \frac{tg(\theta )+1}{1-tg(\theta )\cdot 1}=2$

$\large tg\left(\theta\right)+1=2\left(1-tg\left(\theta\right)\right)$

$\large tg\left(\theta\right)+1=2-2\cdot tg\left(\theta\right)$

$\large 3\cdot tg\left(\theta\right)=1$

$\large tg\left(\theta\right)=\frac{1}{3}$

Gabarito: B

Questão 42

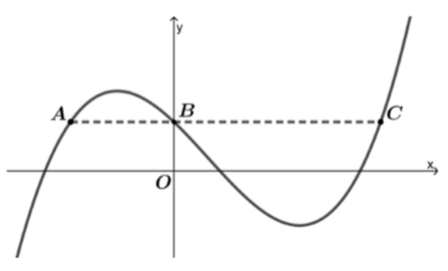
Seja a função polinomial do terceiro grau $\large f\left(x\right)=x^3-x^2-2x+1$ , definida para todo número real $\large x$ . A figura abaixo exibe o gráfico de $\large y=f(x)$ , no plano cartesiano, em que os pontos, A, B, e C têm a mesma ordenada. A distância entre os pontos A e C é igual a:

a) 2

b) $\large 2\sqrt{2}$

c) 3

d) $\large 3\sqrt{2}$

Resolução Comentada

Como todos os pontos $\large (A,B,C)$ representam mesma ordenada, vamos calcular o valor dessa ordenada por meio da ordenada de B, uma vez que ele está no eixo vertical e, portanto, sabemos que sua abcissa é nula $\large (x=0)$ .

Ordenada de B

$\large f\left(x\right)=x^3-x^2-2x+1$

$\large f\left(0\right)=0^3-0^2-2\cdot0+1$

$\large f\left(0\right)=1$

$\large B=\left(0;1\right)$

Além disso, sabemos que as ordenadas de A e de C são dadas por $\large f(x)=1$ , ou seja:

$\large f(x)=1$

$\large x^3-x^2-2x+1=1$

$\large x^3-x^2-2x=0$

$\large x\left(x^2-x-2\right)=0$

Como o produto é nulo, temos duas possibilidades:

$\large x=0$

$\large x^2-x-2=0$

$\large \Delta = b^{2}-4\cdot a\cdot c=-1^{2}-4\cdot 1\cdot (-2)=1+8=9$

$\large x=\frac{-b\pm \Delta }{2\cdot a}=\frac{-(-1)\pm \sqrt{9}}{2\cdot 1}=$

$\large \left\{\begin{matrix}x^\prime=\frac{1+3}{2}=2\\\ \\x^{\prime\prime}=\frac{1-3}{2}=-1\\\end{matrix}\right.$

Gabarito: C

Questão 43

Sabendo que c é um número real, considere, no plano cartesiano, a circunferência de equação $\large x^2+y^2=2cx$ . Se o centro dessa circunferência pertence à reta de equação $\large x+2y=3$ , então seu raio é igual a:

a) $\large \sqrt{2}$

b) $\large \sqrt{3}$

c) 2

d) 3

Resolução Comentada

Para deixarmos a cônica mais explícita, vamos completar quadrados e reescrevê-la de modo mais evidente.

$\large x^2+y^2=2cx$

$\large x^2-2cx+y^2=0$

$\large x^2-2cx+c^2+y^2=0+c^2$

$\large \left(x-c\right)^2+y^2=c^2$

$\large c=raio$

$\large Centro=\left(c,0\right)$

Como o centro deve estar de acordo com a equação da reta fornecida, podemos colocar as coordenadas $\large \left(c,0\right)$ na equação da reta $\large x+2y=3$ .

$\large x+2y=3$

$\large c+2\cdot0=3$

$\large c=3$

$\large raio=3$

Gabarito: D

Questão 44

Se um tetraedro regular e um cubo têm áreas de superfície iguais, a razão entre o comprimento das arestas do tetraedro e o comprimento das arestas do cubo é igual a

a) $\large \sqrt2\sqrt3$

b) $\large \sqrt[4]{2}\sqrt3$

c) $\large \sqrt2\sqrt[4]{3}$

d) $\large \sqrt[4]{2}\sqrt[4]{3}$

Resolução Comentada

Lembrando que a área do tetraedro é dada por quatro vezes a área do triângulo equilátero de aresta $\large a_{T}$ , temos:

$\large A_{T}=\cancel 4\cdot \frac{a_{T}^{2}\sqrt{3}}{\cancel4}$

$\large A_{T}=a_{T}^{2}\sqrt{3}$

Seguindo a orientação de igualar as áreas, temos:

$\large A_T=A_C$

$\large a_T^2\sqrt3=6\cdot l_C^2$

$\large \frac{a_T^2}{a_C^2}=\frac{6}{\sqrt3}\cdot\frac{\sqrt3}{\sqrt3}$

$\large \frac{a_T^2}{a_C^2}=\frac{6\sqrt3}{3}$

$\large \frac{a_T^2}{a_C^2}=2\sqrt3$

$\large \sqrt{\frac{a_T^2}{a_C^2}}=\sqrt{2\sqrt3}$

$\large \left|\frac{a_T}{a_C}\right|=\sqrt2\sqrt[4]{3}$

$\large \frac{a_T}{a_C}=\sqrt2\sqrt[4]{3}$

Gabarito: C

É isso, pessoal! Espero que tenham curtido a resolução da prova de Matemática da prova do Vestibular UNICAMP 2020. Sigam-me nas redes sociais. Têm muitas dicas lá. Mande uma mensagem, caso tenha tido alguma dúvida. Abraços!

Instagram: @professor.marcal

Confira também os cursos e simulados preparatórios do Estratégia Vestibulares para conquistar a vaga dos seus sonhos!

ESTRATÉGIA VESTIBULARES

CURSOS PARA UNICAMP

Prova Unicamp 2020 – Matemática – Resolução Comentada