Fala, pessoal… Tudo bem? Sou o prof. Victor So, do Estratégia Vestibulares e Carreiras Militares. Neste artigo, você vai conferir a resolução das questões da prova de Matemática do ITA 2020. Também deixei disponível a correção em PDF. Assim, você vai poder baixar gratuitamente. Vamos nessa??
Prova ITA 2020
Sejam números reais tais que
e
. Então, o produto
é igual a:
a) 6.
b) 8.
c) 10.
d) 12.
e) 14.
Resolução Comentada
Os números reais podem ser escritos como:
Assim, fazendo o produto entre eles, obtemos:
Podemos usar a seguinte propriedade dos logaritmos para simplificar a expressão:
Reorganizando os termos da expressão:
Gabarito: A
Questão 42
Sejam ,
e
números reais,
, tais que
. Se
,
e
formam, nessa ordem, uma progressão geométrica de razão
, então o produto
e a soma
de todos os possíveis valores para
são iguais a:
a) e
b) e
c) e
d) e
e) e
Resolução Comentada
Vamos reescrever a sequência como
para simplificar as contas.
Assim, a partir do enunciado, podemos escrever:
Como , implica que
Dessa forma, temos:
Façamos
ou
Como k é um número real, temos que
Assim, e
Gabarito: D
Questão 43
A parte real da soma infinita da progressão geométrica cujo termo geral é dado por
é igual a
a)
b)
c)
d)
e)
Resolução Comentada
Note que podemos escrever o termo geral da seguinte forma:
Usando o termo geral, temos a seguinte sequência:
Logo, a razão da PG é:
Como , temos que a soma infinita converge. Assim, usando a fórmula da soma infinita da PG, obtemos:
Multiplicando o numerador e o denominador pelo conjugado do denominador, temos:
A parte real da soma infinita é dada por:
Simplificando a expressão:
Gabarito: A
Questão 44
Duas curvas planas e
são definidas pelas equações
Sejam e
os pontos de interseção de
como o eixo
e
e
os pontos de interseção de
como o eixo
. A área do quadrilátero convexo de vértices P, Q, R e S é igual a:
a)
b)
c)
d)
e)
Resolução Comentada
Inicialmente, devemos encontrar as coordenadas dos pontos P, Q, R, S. Como P e Q são os pontos de interseção de como eixo x, temos:
e
Fazendo na equação de
Portanto, as raízes são ou
.
Assim, temos os pontos e
.
Resta encontrar R e S. Como esses pontos são a interseção de como o eixo y, temos
e
. Fazendo
em
:
Assim, temos e
.
Esboçando os pontos no plano cartesiano, temos a seguinte figura:
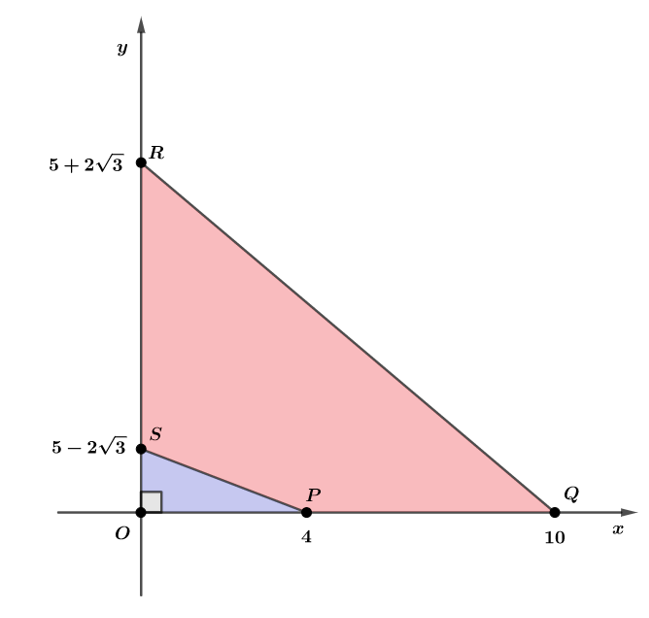
A área pedida é dada por:
Gabarito: C
Questão 45
A cada aniversário, seu bolo tem uma quantidade de velas igual à sua idade. As velas são vendidas em pacotes com 12 unidades e todo ano é comprado apenas um novo pacote. As velas remanescentes são guardadas para os anos seguintes, desde o seu primeiro aniversário. Qual a sua idade, em anos, no primeiro ano em que as velas serão insuficientes?
a) 12.
b) 23.
c) 24.
d) 36.
e) 38.
Resolução Comentada
Veja que a quantidade de velas gastas a cada aniversário pode ser vista como uma progressão aritmética de razão 1.
Assim, o total de velas gastas até o n-ésimo aniversário é:
Como todo ano um novo pacote de 12 velas é compradas, temos até o n-ésimo aniversário:
velas remanescentes
O primeiro ano em que as velas serão insuficientes ocorrerá quando as velas remanescentes satisfazerem a condição:
Sendo n a idade, temos que , logo:
.
Gabarito: C
Questão 46
Seja A um ponto externo a circunferência de centro O e raio r. Considere uma reta passando por A e secante a
nos pontos C e D tal que o segmento AC é o externo a
e tem comprimento igual a r. Seja B o ponto de
tal que O pertence ao segmento AB. Se o ângulo
mede 10°, então a medida do ângulo
é igual a:
a) 25°.
b) 30°.
c) 35°.
d) 40°.
e) 45°.
Resolução Comentada
De acordo com o enunciado, temos a seguinte figura:
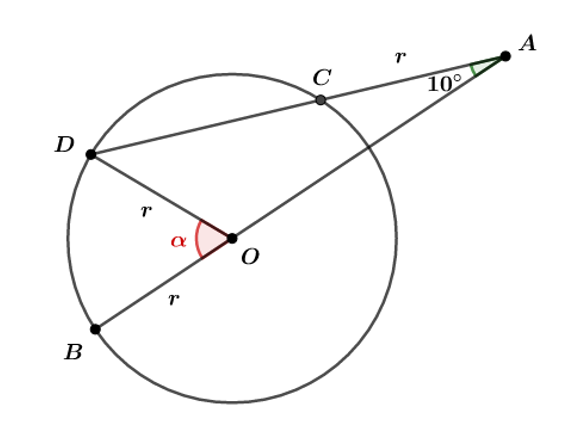
Queremos determinar . Perceba que OCA é um triângulo isósceles, pois
. Logo:
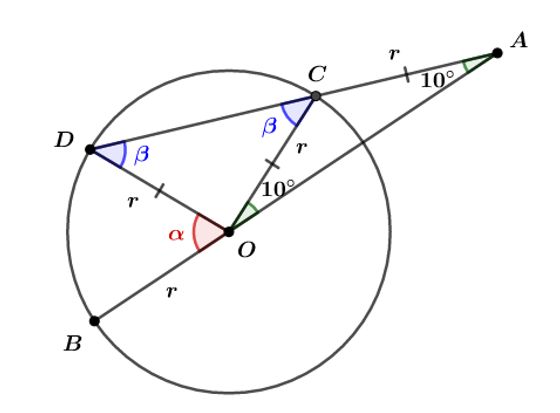
Como é ângulo externo ao
, então
. Sabendo que a soma dos ângulos internos de um triângulo deve ser 180°, temos:
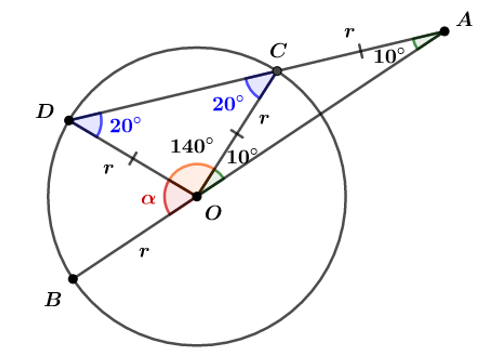
Assim, é dada por:
Gabarito: B
Questão 47
Se um número real satisfazendo
. Então, a soma de todos os valores de
que satisfazem a equação
é igual a
a)
b)
c)
d)
e)
Resolução Comentada
Reescrevendo a equação, obtemos:
Note que
Substituindo na equação:
Assim, temos as seguintes soluções:
ou
Para o intervalo e lembrando que
Somando-se as soluções:
Gabarito: E
Questão 48
Considere o polinômio , sendo m,n números reais fixados. Sabe-se que toda raiz
, com
, da equação
satisfaz a igualdade
. Então, a soma dos quadrados das raízes de
é igual a:
a) 6.
b) 7.
c) 8.
d) 9.
e) 10.
Resolução Comentada
Pelo teorema fundamental da álgebra, o polinômio possui 3 raízes. Além disso, como os coeficientes do polinômio são reais, se tivermos uma raiz complexa, pelo teorema da raiz complexa conjugada, podemos afirmar que o conjugado dessa raiz também é raiz. Assim, temos as seguintes possibilidades:
I) duas raízes complexas e uma real
II) três raízes reais
Para o caso II de apenas raízes reais, temos da condição do enunciado, que toda raiz satisfaz a igualdade
, ou seja, as raízes reais implicam
. Logo, todas as raízes são:
Aplicando a relação de Girard para a soma do produto dois a dois:
Mas, como :
Portanto, chegamos a um absurdo!
A única possibilidade é a I, duas raízes complexas conjugadas e uma real. Então, sejam as raízes, para :
Da condição do enunciado:
Da e
, temos
, logo:
Se , teremos raízes reais, portanto,
.
Como , temos
O polinômio é:
Aplicando Girard:
Usando a na
:
Substituindo na
:
Assim, a soma dos quadrados das raízes é:
Gabarito: B
Questão 49
A expansão decimal do número possui muitos algarismos iguais a zero. Contando da direita para a esquerda, a partir do dígito das unidades, o número de zeros, que esse número possui antes de um dígito não nulo aparecer, é igual a
a) 20.
b) 21.
c) 22.
d) 23.
e) 24.
Resolução Comentada
Seja a fatoração em primos, única pelo teorema fundamental da álgebra, de :
Mas
Dado um número inteiro positivo N, a quantidade de zeros em seu final é igual ao número de vezes em que se pode dividir por 10 e continuar com um inteiro positivo. A cada divisão, diminui-se uma unidade dos expoentes de 2 e de 5. Logo, é possível dividir por vezes.
Acontece que em m!, para todo inteiro positivo m, temos sempre que o expoente de 5 é menor ou igual ao expoente de 2, isto é, . Logo,
. O problema agora é descobrir o expoente de 5 em 100!
Contemos as contribuições de cada .
Cada múltiplo de 5 contribui com pelo menos um fator 5.
Cada múltiplo de contribui com um fator 5 extra.
Não existem múltiplos de com
.
Temos zeros no fim de 100!.
Gabarito: E
Questão 50
Seja um polinômio com coeficientes reais. Sabendo que:
I – é divisível por
;
II – a soma das raízes de é igual a 1;
III – o produto das raízes de é igual a 3;
IV –
então, é igual a
a)
b)
c)
d)
e)
Resolução Comentada
De cada afirmação, temos:
I) Como é divisível por
, temos:
As raízes do polinômio são
, desse modo:
II) Por Girard:
III) Por Girard:
IV) Substituindo no polinômio
Para e
, temos o seguinte sistema:
Multiplicando a última equação por 2:
Somando a primeira equação com a segunda e a primeira com a terceira:
e
Queremos , logo:
Gabarito: D
Questão 51
Os pontos e
são vértices do triângulo isósceles ABC de base BC, contido no primeiro quadrante. Se o raio da circunferência inscrita no triângulo mede 3, então as coordenadas do vértice A são:
a)
b)
c)
d)
e)
Resolução Comentada
Como ABC é um triângulo isósceles, então sua altura em relação ao vértice A também é mediatriz em relação à base BC. Temos a seguinte figura:
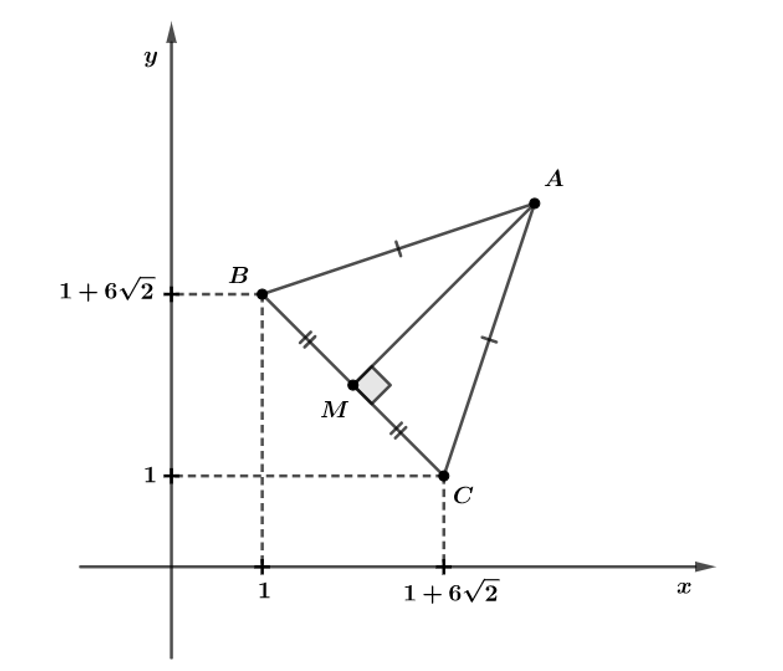
M é ponto médio de BC, logo:
Como é mediatriz, temos que ela é perpendicular à reta
, vamos encontrar seu coeficiente angular:
Como e
, temos que a reta que passa por M e A é y=x, ou seja, as coordenadas de A são da forma
Vamos resolver o problema por geometria plana. Sabemos que é o raio da circunferência inscrita ao triângulo. Consideremos a seguinte figura:
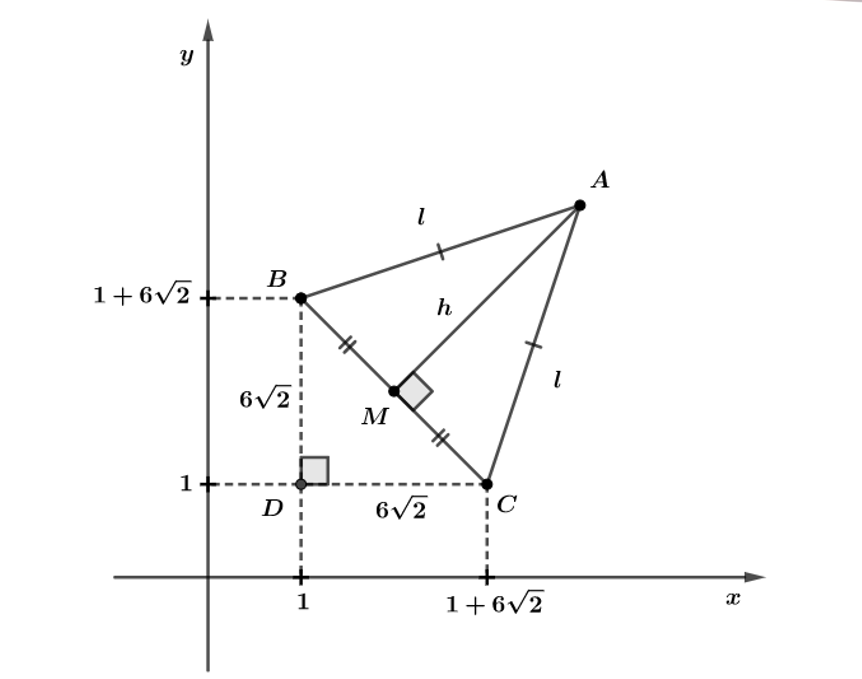
Do triângulo retângulo BCD:
Podemos calcular a área do de duas formas:
Veja que pelo teorema de Pitágoras no
Usando :
Podemos usar a seguinte figura para calcular as coordenadas de A:
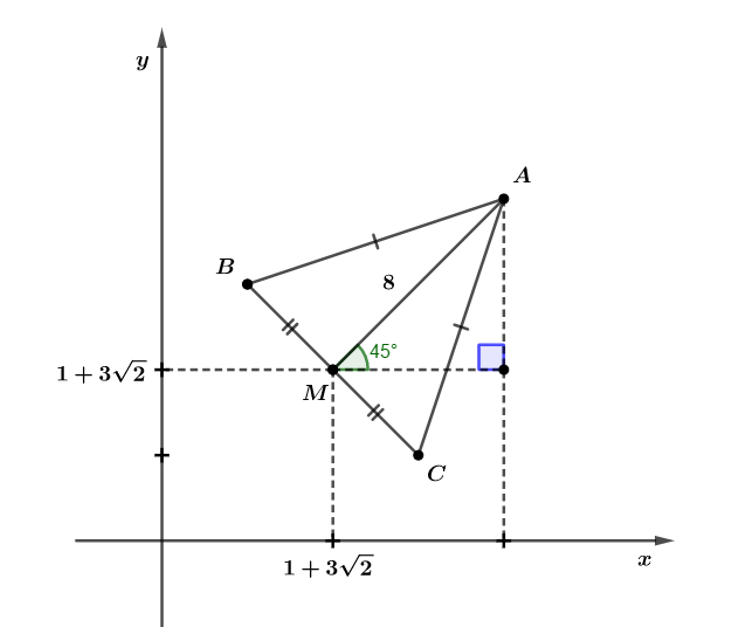
Gabarito: C
Questão 52
Dado , defina
e
e considere as seguintes afirmações:
I. se p ou q é irracional, então a é irracional.
II. se p e q são racionais, então a é racional.
III. se q é irracional, então p é irracional.
É(são) VERDADEIRA(S)
a) apenas I.
b) apenas II.
c) apenas I e II.
d) apenas I e III.
e) todas.
Resolução Comentada
I. Temos da afirmação . Usando sua contrapositiva:
Assim, temos que verificar se implica que
e
. Como
, temos
e
,
e
. Portanto, afirmação verdadeira.
II. Multiplicando-se p por a, temos:
Podemos escrever e
como:
Substituindo em ap:
Para :
Se , temos que
, logo,
.
Para :
Portanto, , logo, não é possível.
Concluímos que a afirmação é verdadeira.
III. Tomemos o seguinte contraexemplo:
Portanto, afirmação falsa.
Gabarito: C
Questão 53
Considere as seguintes afirmações:
- I. Todo poliedro formado por 16 faces quadrangulares possui exatamente 18 vértices e 32 arestas.
- II. Em todo poliedro convexo que possui 10 faces e 16 arestas, a soma dos ângulos de todas as faces é igual a 2160°.
- III. Existe um poliedro com 15 faces, 22 arestas e 9 vértices.
É(são) VERDADEIRA (S)
a) apenas I.
b) apenas II.
c) apenas III.
d) apenas I e II.
e) apenas II e III.
Resolução Comentada
I. Cuidado quando a afirmação diz “todo poliedro”, pois podemos ter um poliedro côncavo que não possui esse número de vértices e arestas. Veja o contraexemplo:
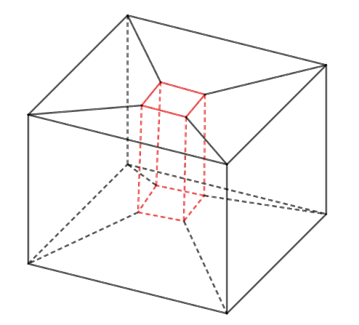
Esse poliedro possui 16 faces quadrangulares, 32 arestas e 16 vértices. Portanto, afirmação falsa.
II. A afirmação diz que o poliedro convexo possui 10 faces e 16 arestas, logo F=10 e A=16. Pela relação de Euler, temos:
A soma dos ângulos internos de um poliedro convexo é dada por:
Portanto, afirmação verdadeira.
III. Se existe um poliedro com tais características, devemos ter:
Note que
Substituindo A=22 e F=15, temos:
Portanto, afirmação falsa.
Gabarito: B
Questão 54
Considere as seguintes afirmações:
I. Sejam três planos distintos, e secantes dois a dois segundo as retas distintas, r, s e t. Se
.
II. As projeções ortogonais de duas retas paralelas r e s sobre um plano são duas retas paralelas.
III. Para quaisquer retas r, s e t reversas duas a duas, existe uma reta u paralela à r e concorrente com s e com t.
É(são) VERDADEIRA(S)
a) apenas I.
b) apenas II.
c) apenas I e II.
d) apenas I e III.
e) nenhuma.
Resolução Comentada
I. Como r,s,t são as retas da interseção dos três planos distintos e secantes dois a dois, temos:
Se e sabendo que as retas são distintas (não podem ser coincidentes), temos:
Logo:
Portanto, . Verdadeira.
II – Podemos ter duas retas paralelas e perpendiculares a um mesmo plano, a projeção delas no plano será dois pontos. Portanto, falsa.
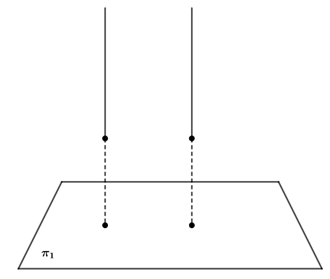
III. Vejamos o contra-exemplo:
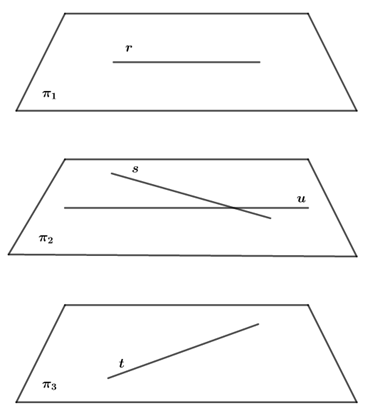
Note que tomando-se os planos e as retas
, não paralelas entre elas, temos que a reta u paralela à r não pode ser concorrente simultaneamente à S e à T. Portanto, falta.
Gabarito: A
Questão 55
Considere o conjunto de todas as matrizes quadradas ordem n x n, com exatamente k, elementos iguais a 1, e os demais iguais a 0 (zero). Escolhendo aleatoriamente matrizes
e
, a probabilidade de que
e
é igual a:
a)
b)
c)
d)
e)
Resolução Comentada
I) Analisemos as matrizes . Como n=3 e k=1, temos uma matriz de ordem 3×3 e um único elemento igual a 1. Temos, por exemplo:
Note que nesse caso, se o elemento 1 estiver na diagonal principal, . Portanto, das 9 posições possíveis, podemos escolher apenas 6 (excluindo-se a diagonal principal) para inserir o elemento 1. Assim, temos:
II) , temos matrizes de ordem 4×4 e 2 elementos 1. Como analisamos no item I, se tivermos um elemento na diagonal principal, a matriz
. Então, para o primeiro elemento 1, temos que ele pode escolher 12 das 16 posições possíveis (excluindo-se a diagonal principal), logo, essa probabilidade é
Para o segundo elemento 1, devemos analisar do seguinte modo. Seja R definido por , assim, temos que os elementos de
serão:
Então, para obtermos uma matriz nula desse produto, temos que o segundo 1 não pode ocupar a diagonal principal (4 casos) e também não pode ocupar as posições que fazem com que , isso ocorre quando a linha do segundo elemento 1 é a coluna do primeiro (3 casos excluindo-se a diagonal principal) e quando a coluna do segundo elemento 1 é a linha do primeiro elemento (2 casos), logo, das 15 posições possíveis para o segundo elemento, temos:
Portanto, a probabilidade pedida é:
Gabarito: B
É isso, pessoal! Espero que tenham curtido a resolução da prova de Matemática da prova da 1ª Fase do Vestibular ITA 2020. Sigam-me nas redes sociais. Têm muitas dicas lá. Mande uma mensagem, caso tenha tido alguma dúvida. Abraços!
Instagram: @profvictorso
Facebook: profvictorso



