Olá, pessoal… Tudo bem? Sou o prof. Marçal, do Estratégia Vestibulares, e escrevo este artigo para resolver as questões da prova da FUVEST 2020, da disciplina de Matemática. Nesta página, você vai conferir a resolução completa e ainda vai poder baixar gratuitamente os comentários em PDF. Vamos nessa??
Navegue pelo conteúdo
Prova FUVEST 2020
Questão 13
Carros que saem da cidade A rumo a alguma das cidades turísticas E, F e G fazem caminhos diversos, passando por pelo menos uma das cidades B, C e D, apenas no sentido indicado pelas setas, como mostra a figura. Os números indicados nas setas são as probabilidades, dentre esses carros, de se ir de uma cidade a outra.
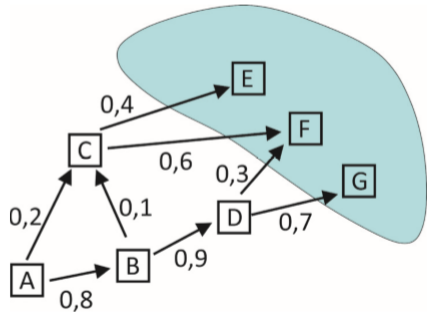
Nesse cenário, a probabilidade de um carro ir de A a F é
(A) 0,120.
(B) 0,216.
(C) 0,264.
(D) 0,336.
(E) 0,384.
Resolução Comentada
Para ir de A a F, há três caminhos possíveis: ACF, ABCF e ABDF.
Em cada caminho, as probabilidades são dadas pelos produtos:
Como os caminhos são todos alternativos, a probabilidade total de o carro ir de A a F é dada pela soma
Gabarito: E
Questão 14
Se, em 15 anos, o salário mínimo teve um aumento nominal de 300% e a inflação foi de 100%, é correto afirmar que o aumento real do salário mínimo, nesse período, foi de
(A) 50%.
(B) 100%.
(C) 150%.
(D) 200%.
(E) 250%.
Resolução Comentada
Considerando o salário x com um crescimento de 300%, ou seja, de 3x, temos:
Já seu poder de compra, sofrendo uma alta de 100%, ou seja, de 1x, temos:
Desse modo, podemos perceber que o salário que tinha uma relação de 1 para 1 com a compra, agora é o dobro da compra. Se o poder de compra é o dobro, sofreu aumento de 100%, indicando o gabarito b).
Podemos, alternativamente, utilizar a fórmula para o ganho real:
Gabarito: B
Questão 15
O cilindro de papelão central de uma fita crepe tem raio externo de 3 cm. A fita tem espessura de 0,01 cm e dá 100 voltas completas. Considerando que, a cada volta, o raio externo do rolo é aumentado no valor da espessura da fita, o comprimento total da fita é de, aproximadamente,
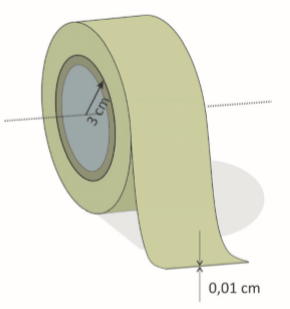
(A) 9,4 m.
(B) 11,0 m.
(C) 18,8 m.
(D) 22,0 m.
(E) 25,1 m.
Note e Adote:
π = 3,14
Resolução Comentada
Sabendo que o comprimento de uma circunferência é dado por , temos a seguinte sequência de comprimentos ao enrolar a fita no cilintro:
Dessa forma, o comprimento total da fita é dado por:
Gabarito: D
Questão 16
Um objeto é formado por 4 hastes rígidas conectadas em seus extremos por articulações, cujos centros são os vértices de um paralelogramo. As hastes movimentam-se de tal forma que o paralelogramo permanece sempre no mesmo plano. A cada configuração desse objeto, associa-se d, a medida do menor ângulo interno do paralelogramo. A área da região delimitada pelo paralelogramo quando d = 90° é A.
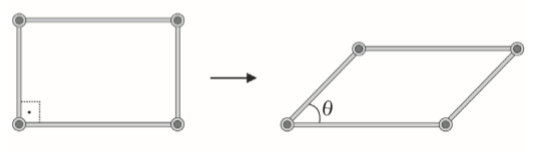
Para que a área da região delimitada pelo paralelogramo seja o valor de
é necessariamente, igual a:
(A) 15°
(B) 22,5°
(C) 30°
(D) 45°
(E) 60°
Resolução Comentada
Chamando os lados do retângulo de x e y, temos a seguinte relação entre suas áreas:
Gabarito: C
Questão 17
A menor esfera na qual um paralelepípedo reto-retângulo de medidas 7 cm x 4 cm x 4 cm está inscrito tem diâmetro de
(A) 9 cm.
(B) 10 cm.
(C) 11 cm.
(D) 12 cm.
(E) 15 cm.
Resolução Comentada
Para que a esfera tangencie todos os vértices do paralelepípedo, seu diâmetro será igual à diagonal do paralelepípedo.
Gabarito: A
Questão 18
A dona de uma lanchonete observou que, vendendo um combo a R$ 10,00, 200 deles são vendidos por dia, e que, para cada redução de R$ 1,00 nesse preço, ela vende 100 combos a mais. Nessas condições, qual é a máxima arrecadação diária que ela espera obter com a venda desse combo?
(A) R$ 2.000,00
(B) R$ 3.200,00
(C) R$ 3.600,00
(D) R$4.000,00
(E) R$ 4.800,00
Resolução Comentada
A arrecadação é dada pelo produto entre o preço de venda e o número de vendas.
Arrecadação =
Como, ao retirar 1 real, ganha-se 100 clientes, ao retirar x reais do preço, ganhar-se-á 100x clientes. Dessa forma, podemos reescrever nossa arrecadação como:
Arrecadação =
Arrecadação =
Arrecadação =
Podemos perceber que a arrecadação depende da variável x de forma quadrática, cuja parábola apresenta concavidade negativa (a<0). Assim, ao tentar maximizar a arrecadação, estamos, na verdade, procurando o vértice da parábola.
Arrecadação =
Gabarito: C
Questão 19
A função E de Euler determina, para cada número natural n, a quantidade de números naturais menores do que n cujo máximo divisor comum com n é igual a 1. Por exemplo, E (6) = 2 pois os números menores do que 6 com tal propriedade são 1 e 5. Qual o valor máximo de E (n), para n de 20 a 25?
(A) 19
(B) 20
(C) 22
(D) 24
(E) 25
Resolução Comentada
A descrição da função de Euler indica que devemos selecionar, a cada número n, todos os números menores que n, que sejam primos com n.
Para n=20, temos:
Para n=21, temos:
Perceba que, por serem números compostos, acabamos por retirar todos os números menores que n que tenham algum primo em comum com n.
Dessa forma, não há necessidade de fazermos o processo para todos os números do exercício (entre 20 e 25), pois, nesse intervalo, só há um primo, o 23.
Assim, para o 23, não precisaremos retirar número algum da sequência dos números menores que ele, pois é primo, resultando no maior resultado possível, nesse intervalo, para E(n).
Portanto, n=23
Gabarito: C
Questão 20
Se para todo número real x, o valor de a+b é:
(A) 3.
(B) 5.
(C) 6.
(D) 9.
(E) 12.
Resolução Comentada
Desenvolvendo os cubos, temos:
O que nos leva ao seguinte sistema de equações
Como a questão solicitou o valor de a+b, não é preciso ir adiante, já temos nossa resposta: a+b=3.
Gabarito: A
Questão 21
Uma agência de turismo vendeu um total de 78 passagens para os destinos: Lisboa, Paris e Roma. Sabe-se que o número de passagens vendidas para Paris foi o dobro do número de passagens vendidas para os outros dois destinos conjuntamente. Sabe-se também que, para Roma, foram vendidas duas passagens a mais que a metade das vendidas para Lisboa. Qual foi o total de passagens vendidas, conjuntamente, para Paris e Roma?
(A) 26
(B) 38
(C) 42
(D) 62
(E) 68
Resolução Comentada
Da leitura do enunciado, tiramos o seguinte sistema de equações:
Dando andamento à resolução do sistema, temos:
Novamente, a questão nos solicitou o valor da soma P+R, portanto, não há necessidade de seguirmos com a resolução do sistema, uma vez que
Gabarito: D
Questão 22
Um ponto (x, y) do plano cartesiano pertence ao conjunto F se é equidistante dos eixos OX e OY e pertence ao círculo de equação .
É correto afirmar que F
(A) é um conjunto vazio.
(B) tem exatamente 2 pontos, um no primeiro quadrante e outro no segundo quadrante.
(C) tem exatamente 2 pontos, ambos no primeiro quadrante.
(D) tem exatamente 3 pontos, sendo dois no primeiro quadrante e outro no segundo quadrante.
(E) tem exatamente 4 pontos, sendo dois no primeiro quadrante e dois no segundo quadrante.
Resolução Comentada
O conjunto de pontos que é equidistante dos eixos coordenados é dado pelas retas
y = x
y = -x
Como, para pertencerem ao conjunto F, os pontos também precisam satisfazer a equação , podemos utilizar a substituição para encontrar as coordenadas dos pontos.
Para o caso y = x
e
Portanto, dois pontos do primeiro quadrante. Vejamos o próximo caso.
Ou seja, um ponto no segundo quadrante.
Até aqui, tudo bem, temos 3 pontos, dois no primeiro quadrante e um no segundo quadrante, o que poderia indicar a alternativa d) como nosso gabarito.
No entanto, a palavra “círculo”, no enunciado, remete à área cercada pela circunferência. Como uma das retas (y=x) é secante à circunferência, teríamos infinitos pontos pertencentes ao conjunto F, não só os 3 que achamos.
Além disso, a equação fornecida, não representa um círculo e sim uma circunferência. Equações de círculo envolvem desigualdades, não igualdades.
Dessa forma, apesar de haver uma indicação de resposta na alternativa d), indico a questão para anulação.
Gabarito: PARA ANULAÇÃO
Questão 23
Uma cidade é dividida em dois Setores: o Setor Sul, com área de 10 km2, e o Setor Norte, com área de 30 km2. Após um final de semana, foram divulgados os seguintes totais pluviométricos:

É correto afirmar que o total pluviométrico desse final de semana na cidade inteira foi de
(A) 15 mm.
(B) 17 mm.
(C) 22 mm.
(D) 25 mm.
(E) 28 mm.
Resolução Comentada
O total pluviométrico P é, na verdade, uma razão entre o volume de chuva que cai em uma determinada área, ou seja, uma razão entre um volume e uma área.
Seguindo essa definição, temos:
Gabarito: D
Questão 24

As possíveis soluções, em polegadas (inches, em inglês), para o problema matemático proposto no quadrinho, no caso em que os pontos A, B e C estão em uma mesma reta, são
(A) e 10
(B) , 5 e 10
(C) e 10
(D) e 10
(E) e 5
Resolução Comentada
O texto deixa claro que a distância entre e
é o dobro da distância entre
e
ou seja
Utilizando um sistema ordenado e respeitando a ordem de que A, B e C são colineares, podemos representar os pontos em uma reta orientada.
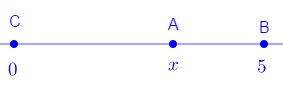
Dessa forma, seguindo as orientações do enunciado, temos:
Até aqui, tudo bem. No entanto, há uma segunda possibilidade para posicionarmos o ponto A, fora do intervalo BC, veja:

Com essa nova representação, mas ainda com a premissa do exercício de que , temos:
Assim, temos duas possibilidades para a posição do ponto A, nas condições dadas.
Gabarito: A
É isso, pessoal! Espero que tenham curtido a resolução da prova de Matemática da prova do Vestibular FUVEST 2020. Sigam-me nas redes sociais. Têm muitas dicas lá. Mande uma mensagem, caso tenha tido alguma dúvida. Abraços!
Instagram: @professor.marcal

Veja também:
- Geometria: o que é e como é classificada
- Figuras Geométricas: planas, espaciais e como aparece nos vestibulares
- Geometria Plana no Enem: conceito e definições
- Semelhança de triângulos
- Geometria analítica: fórmulas, gráficos e equações
- Geometria Espacial: conheça os sólidos e fórmulas
- Progressão aritmética: o que é, fórmulas, usos e exemplos
- Resolução da prova de Matemática da 2ª Fase da Unicamp 2020
- Prova UNESP 2020 – Matemática – Resolução Comentada



