Olá, pessoal… Tudo bem? Sou o prof. Marçal Ferreira, professor de Matemática do Estratégia Vestibulares. Escrevo este artigo para resolver as questões da prova da 2ª Fase do vestibular da UNESP 2020. Nesta página, você vai conferir a resolução completa e ainda vai poder baixar gratuitamente os comentários em PDF.
UNESP 2ª Fase – Matemática
Questão 22
Um grupo de cientistas estuda os hábitos de uma espécie animal em uma área de preservação. Inicialmente, delimitou-se uma área plana (ABCD, figura 1), na qual deverão ser estabelecidos dois pontos de observação. Afigura 2 apresenta um modelo matemático da área delimitada, com dois setores retangulares nos quais serão estabelecidos os pontos de observação, sendo que cada ponto de observação deverá pertencer a apenas um dos setores. Parte do grupo de cientistas ocupar-se-á exclusivamente com os hábitos de reprodução dessa espécie e atuará na região em forma de paralelogramo, indicada na figura 3.
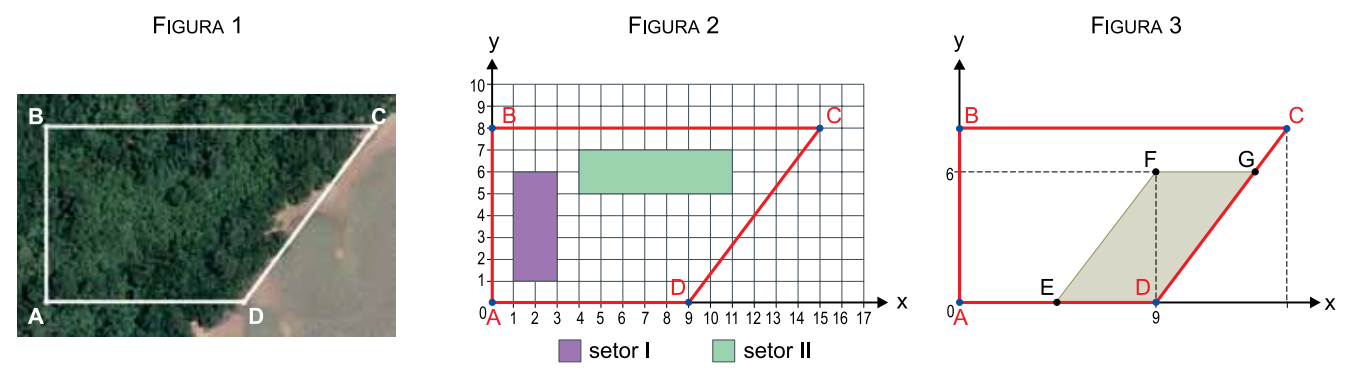
a) Para a construção dos dois pontos de observação, considere que a localização do ponto do setor I deverá ser equidistante dos pontos A e B e que a localização do ponto do setor II deverá ser equidistante dos pontos B e C. Utilizando as coordenadas do plano cartesiano da figura 2, determine uma possível localização do ponto de observação para cada um dos setores.
b) Dado que 1 unidade de distância dos planos cartesianos equivale a 200 metros de distância real, determine o perímetro da região em que serão estudados os hábitos de reprodução da espécie (figura 3).
Resolução
a) Para a construção dos dois pontos de observação, considere que a localização do ponto do setor I deverá ser equidistante dos pontos A e B e que a localização do ponto do setor II deverá ser equidistante dos pontos B e C. Utilizando as coordenadas do plano cartesiano da figura 2, determine uma possível localização do ponto de observação para cada um dos setores.
Os pontos equidistantes de A e de B são dados pela reta y=4. Como, pelo enunciado, o setor I tem valores de x tais que 1<x<3, uma possível localização do ponto de observação é (2;4).
Os pontos equidistantes de B e de C são dados pela reta x=7,5. Como, pelo enunciado, o setor II tem valores de y tais que 5<y<7, uma possível localização do ponto de observação é (7,5;6).
b) Dado que 1 unidade de distância dos planos cartesianos equivale a 200 metros de distância real, determine o perímetro da região em que serão estudados os hábitos de reprodução da espécie (figura 3).
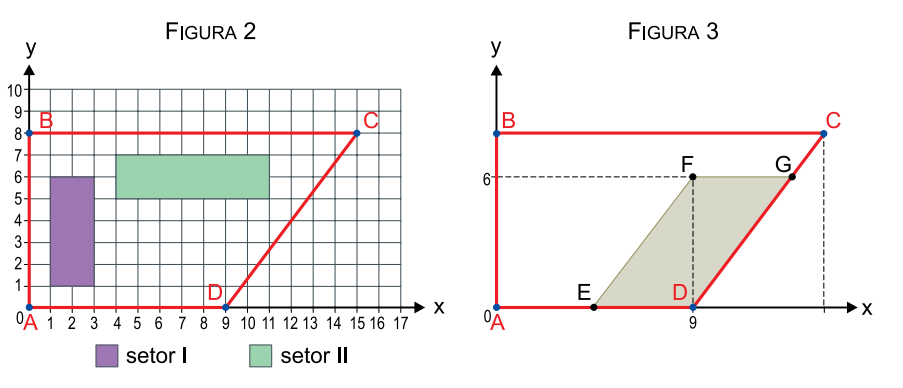
As coordenadas dos pontos D,E,F,G são:
D = (9; 0)
G = (13,5; 6)
F = (9; 6)
E = (4,5 ; 0)
Chamando x a distância DG, temos:
Dessa forma, o perímetro P, em metros, é dado por:
Questão 23
A modelagem dos sistemas de cor é essencial na computação gráfica, e um dos maiores desafios dessa área é a conversão de coordenadas de diferentes sistemas. O sistema RGB pressupõe que o sistema de processamento de cor do olho humano seja baseado nas faixas vermelha (red). verde (green) e azul (blue) do espectro visível Já o modelo CMY usa cores complementares, ciano (cyan), magenta (magenta) e amarelo (yellow), e foi importante no desenvolvimento de impressoras As cores no sistema CMY ficam delimitadas por um cubo, o cubo CMY, conforme ilustrado
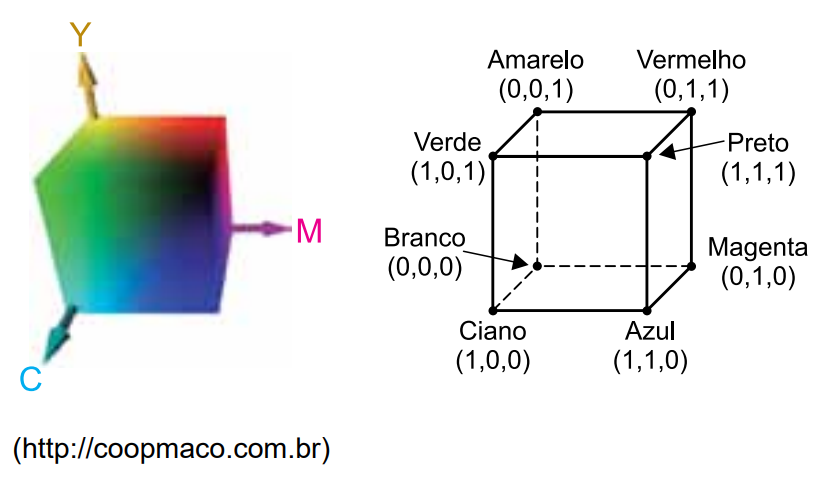
a) A transformação de uma cor no sistema RGB, descrita por (r, g, b), para o sistema CMY, descrita por (c, m, y), é dada por . Supondo que uma cor no sistema RGB seja descrita por
, apresente as coordenadas dessa cor o sistema CMY e indique qual das oito cores detalhadas no cubo CMY está mais próxima dela.
b) O sistema NTSC (National Television Standards Committee), utilizado em emissões para a televisão, baseia-se na separação dos sinais de cor RGB em um sinal de luminosidade e dois sinais de cromaticidade Assim como no espaço RGB, as cores no espaço YIQ, utilizado no sistema NTSC, são descritas por coordenadas, sendo representadas por (y, i, q). A relação entre as cores desses dois sistemas é dada, de modo simplificado, pela expressão matricial:
Sabendo que uma cor no sistema RGB descrita por (0,2; 0,5, 0,4) está associada a uma cor no sistema YIQ descrita por (0,4, -0,15; -0,33), determine ,
e
.
Resolução
a) Utilizando a equação matricial fornecida no enunciado, temos:
Assim, as coordenadas dessa cor no sistema CMY são e a cor no cubo que está mais próxima dela é o preto.
b) Utilizando a equação matricial fornecida, temos:
Assim, os valores de ,
e
são tais que
.
Questão 24
A penicilina benzatina é um antibiótico indicado no tratamento de certas infecções, e sua meia-vida é de 336 horas. Ou seja, após esse período de tempo a quantidade de medicamento no sangue reduz-se pela metade. O tratamento convencional é feito com uma aplicação de 1200000 Ul do medicamento e essa dose mantém-se em quantidade adequada no sangue (isto é, não inferior a 300000 Ul) durante os 28 dias seguintes. A dosagem, o número de doses e o intervalo de tempo entre as doses depende da doença a ser tratada.
a) Considere um paciente que recebeu 2 doses, cada uma de 1200000 Ul, desse medicamento, sendo que a segunda dose foi aplicada 28 dias após a primeira dose. Faça um esboço gráfico na malha presente no campo de Resolução e Resposta, representando a quantidade desse medicamento no sangue ao longo de 8 semanas de tratamento.
b) Considere outro caso, em que um paciente foi tratado com 2 doses, cada uma de 2400000 Ul, de penicilina benzatina, sendo a segunda dose aplicada 14 dias após a primeira. Determine a quantidade desse medicamento no sangue do paciente, em Ul, logo após ele tomar a segunda dose e indique durante quantos dias completos, após essa segunda dose, a quantidade de medicamento permanecerá em quantidade adequada no sangue desse paciente. Adote em seus cálculos log2 = 0,30; log3 = 0,48
Resolução
O tempo de meia vida de horas é equivalente a dias, ou seja, 14 dias, ou ainda, semanas.
Dessa forma, a progressão em UI a cada duas semanas é a seguinte:
Colocando esses valores no gráfico, temos:
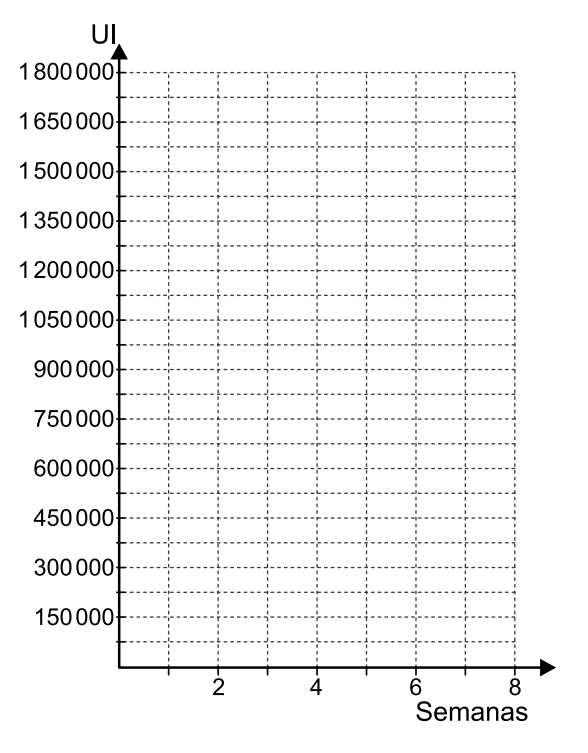
b) Inicialmente, temos a seguinte progressão:
Assim, a quantidade desse medicamento no sangue do paciente, em UI, logo após ele tomar a segunda dose é de 3 600 000 UI.
Calculando a quantidade n de períodos de meia vida para que a concentração não seja superior a 300 000 UI:
Como cada período de meia vida é de 14 dias, temos:
Assim, a quantidade permanece adequada até 50 dias após o paciente tomar a segunda dose.
É isso, pessoal! Espero que tenham curtido a resolução da prova de Matemática da prova do Vestibular UNESP 2020. Sigam-me nas redes sociais. Têm muitas dicas lá. Mande uma mensagem, caso tenha tido alguma dúvida.
Você também pode baixar essa resolução em PDF. Basta clicar no link a seguir. Abraços!
Abraços!
Instagram: @professor.marcal



