Resolução Comentada da prova de Física FUVEST 2020

Olá, caro aluno. Seja Bem-Vindo. Sou o prof. Lucas Costa, e escrevo este artigo, com a ajuda do prof. Toni Burgatto, para disponibilizar a você a resolução das questões da prova de Física FUVEST 2020, 1ª fase.

Durante a leitura deste artigo, você vai conferir o que cobravam as questões e como você teria que resolver até chegar ao Gabarito sugerido pela FUVEST. Vamos nessa?

">Prova FUVEST Física – Resolução" class="wp-block-file__button" download>Baixar

Navegue pelo conteúdo

Prova de Física FUVEST 2020

Questão 69

Em julho de 1969, os astronautas Neil Armstrong e Buzz Aldrin fizeram o primeiro pouso tripulado na superfície da Lua, enquanto seu colega Michael Collins permaneceu a bordo do módulo de comando Columbia em órbita lunar. Considerando que o Columbia estivesse em uma órbita perfeitamente circular a uma altitude de 260km acima da superfície da Lua, o tempo decorrido (em horas terrestres ‐ h) entre duas passagens do Columbia exatamente acima do mesmo ponto da superfície lunar seria de

(A) 0,5 h.

(B) 2 h.

(D) 8 h.

(E) 72 h.

Note e adote:
Constante gravitacional: G ≅ 9 x 10^-13 km³ / (kg h²);
Raio da Lua = 1.740km
Massa da Lua ≅ 8 x 10²² kg;
π ≅ 3

Resolução Comentada

Quando um satélite se movimenta em uma trajetória circular em torno de algum astro, a força gravitacional atuará como força resultante centrípeta. A questão pede o período de rotação da nave. Devemos igualar a força gravitacional à força centrípeta, escrevendo a velocidade angular em função do período:

$\large \vec{F}_{cp}=\vec{F}_{grav}$

$\large m_{corpo}\cdot\omega^2\cdot R=G\cdot\frac{m_{corpo}\cdot m_{Lua}}{d^2}$

$\large \cancel{m_{corpo}}\cdot\omega^2\cdot R=G\cdot\frac{\cancel{m_{corpo}}\cdot m_{Lua}}{d^2}$

Note que o raio da trajetória centrípeta será dada pela soma do raio da lua com a altitude da nave em relação à Lua. Podemos que o raio da trajetória será a distância de separação entre os dois corpos:

$\large \omega^2\cdot d=G\cdot\frac{m_{Lua}}{d^2}$

$\large \omega^2=G\cdot\frac{m_{Lua}}{d^3}$

$\large \omega=\sqrt{G\cdot\frac{m_{Lua}}{d^3}}$

Agora precisamos nos lembrar da relação entre a velocidade angular $\large \omega$ e o período $\large T$ :

$\large \omega=\frac{2\cdot\pi}{T}$

Voltando à relação anterior:

$\large \frac{2\cdot\pi}{T}=\sqrt{G\cdot\frac{m_{Lua}}{d^3}}$

$\large \frac{T}{2\cdot\pi}=\frac{1}{\sqrt{G\cdot \frac{m_{Lua}}{d^3}}}$

$\large T=\frac{2\cdot\pi}{\sqrt{G\cdot\frac{m_{Lua}}{d^3}}}=2\cdot\pi\cdot\sqrt{\frac{d^3}{G\cdot m_{Lua}}}$

Agora devemos substituir os valores fornecidos:

$\large T=2\cdot3\cdot\sqrt{\frac{\left(1740+260\right)^3}{9\cdot{10}^{-13}\cdot8\cdot{10}^{22}\ }}=6\cdot\sqrt{\frac{\left(2000\right)^3}{9\cdot8\cdot{10}^9\ }}$

$\large T=6\cdot\sqrt{\frac{\left(2\cdot{10}^3\right)^3}{9\cdot8\cdot{10}^9\ }}=6\cdot\sqrt{\frac{\cancel{(8\cdot 10^{9})}}{9\cdot \cancel{8\cdot 10^{9}}}}$

$\large T=6\cdot\sqrt{\frac{1}{9\ }}=6\cdot\frac{1}{3}=2\ h$

Gabarito: B

Questão 70da prova de Física FUVEST 2020

Em 20 de maio de 2019, as unidades de base do Sistema Internacional de Unidades(SI) passaram a ser definidas a partir de valores exatos de algumas constantes físicas. Entre elas, está a constante de Planck h, que relaciona a energia E de um fóton (quantum de radiação eletromagnética) coma sua frequência f na forma E=hf. A unidade da constante de Planck em termos das unidades de base do SI (quilograma, metro e segundo) é:

(A) kg m²/s

(B) kg s/m²

(D) kg sm

(E) kg m²/s³

Resolução Comentada

Devemos fazer a análise dimensional da relação de Planck:

$\large E=h\cdot f$

$\large \left[J\right]=h\cdot\left[Hz\right]$

$\large h=\left[J\right]/\left[Hz\right]$

Devemos nos lembrar, por exemplo, que o trabalho de uma força, medido em J, é dado pelo produto entre força e distância. Também devemos nos lembrar que o Hz equivale ao inverso do segundo:

$\large h=Trabalho/\left[1/s\right]$

$\large h=Trabalho\cdot\left[s\right]$

$\large h=F\cdot d\cdot\left[s\right]$

$\large h=F\cdot\left[m\right]\cdot\left[s\right]$

Também convêm nos lembrarmos que a segunda lei de Newton diz que a força é dada pelo produto entre massa e aceleração:

$\large h=m\cdot a\cdot\left[m\right]\cdot\left[s\right]$

$\large h=\left[kg\right]\cdot\left[\frac{m}{s^2}\right]\cdot\left[m\right]\cdot\left[s\right]$

$\large h=\left[\frac{kg\cdot m^2}{s}\right]$

Gabarito: A

Questão 71

A transmissão de dados de telefonia celular por meio de ondas eletromagnéticas está sujeita a perdas que aumentam com a distância d entre a antena transmissora e a antena receptora. Uma aproximação frequentemente usada para expressar a perda L, em decibéis (dB), do sinal em função de d, no espaço livre de obstáculos, é dada pela expressão

$\large L=20\ log_{10}\left ( \frac{4\pi d}{\lambda } \right )$

em que $\large \lambda$ é o comprimento de onda do sinal. O gráfico a seguir mostra L em (dB) versus d (em metros) para um determinado comprimento de onda $\large \lambda$ .

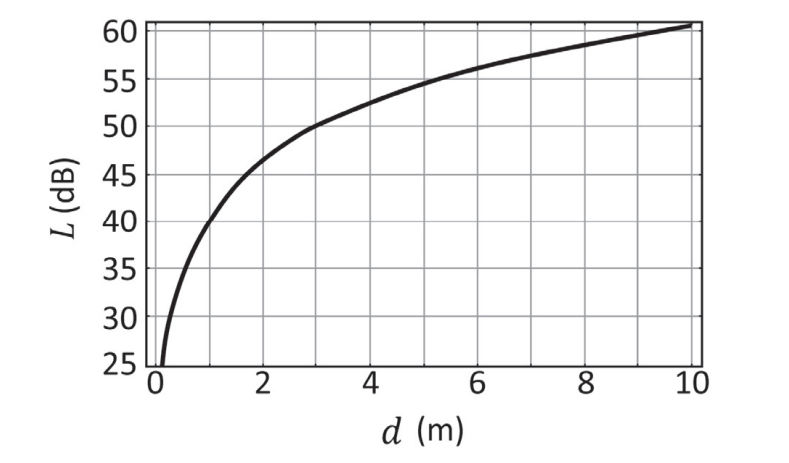
Com base no gráfico, a frequência do sinal é aproximadamente

(A) 2,5 GHz.

(B) 5 GHz.

(D) 40 GHz.

(E) 100 GHz.

Note e adote:
Velocidade da luz no vácuo: c = 3 x 10⁸ m/s
π ≅ 3
1 GHz = 10⁹ Hz

Resolução Comentada

Pelo gráfico, para a distância de 1m, temos a perda L de 40 dB:

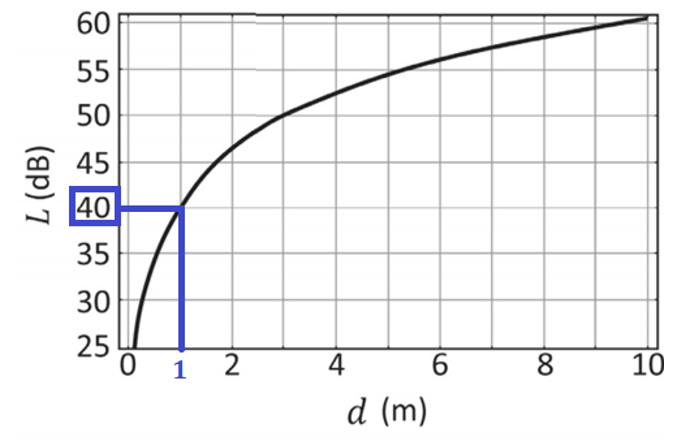
Usando a relação fornecida no enunciado podemos determinar o comprimento de onda para depois usarmos a equação fundamental da ondulatória e determinarmos a sua frequência:

$\large L=20\cdot\log_{10}{\left(\frac{4\cdot\pi\cdot d}{\lambda}\right)}$

$\large 40=20\cdot\log_{10}{\left(\frac{4\cdot3\cdot1}{\lambda}\right)}$

$\large \frac{40}{20}=\log_{10}{\left(\frac{12}{\lambda}\right)}$

$\large 2=\log_{10}{\left(\frac{12}{\lambda}\right)}$

Pela propriedade fundamental do logaritmo, temos:

$\large {10}^2=\frac{12}{\lambda}$

$\large \lambda=\frac{12}{{10}^2}$

Agora devemos usar a equação fundamental da ondulatória:

$\large c=\lambda\cdot f\Rightarrow f=\frac{c}{\lambda}$

Usando o comprimento de onda encontrado, e a velocidade da luz fornecida no “Note e adote”, temos:

$\large f=\frac{c}{\lambda}=\frac{3\cdot{10}^8}{\frac{12}{{10}^2}}=3\cdot{10}^8\cdot\frac{{10}^2}{12}=$

$\large \frac{30\cdot{10}^9}{12}=2,5\cdot{10}^9Hz=2,5\ GHz$

Gabarito: A

Questão 72

Um estímulo nervoso em um dos dedos do pé de um indivíduo demora cerca de 30 ms para chegar ao cérebro. Nos membros inferiores, o pulso elétrico, que conduz a informação do estímulo, é transmitido pelo nervo ciático, chegando à base do tronco em 20 ms. Da base do tronco ao cérebro, o pulso é conduzido na medula espinhal. Considerando que a altura média do brasileiro é de 1,70 m e supondo uma razão média de 0,6 entre o comprimento dos membros inferiores e a altura de uma pessoa, pode‐se concluir que as velocidades médias de propagação do pulso nervoso desde os dedos do pé até o cérebro e da base do tronco até o cérebro são, respectivamente:

(A) 51 m/s e 51 m/s

(B) 51 m/s e 57 m/s

(D) 57 m/s e 68 m/s

(E) 68 m/s e 68 m/s

Resolução Comentada

Devemos usar a equação da velocidade para o movimento uniforme, considerando os dados fornecidos:

$\large v_{dedo}=\frac{\Delta S_{dedo}}{\Delta t_{dedo}}=\frac{1,7}{30\cdot{10}^{-3}}=$

$\large \frac{1,7\cdot{10}^3}{30}=\frac{1700}{30}=\frac{170}{3}\cong57\ m/s$

Se a razão média entre o comprimento dos membros inferiores e a altura da pessoa é de 0,6, temos que os membros superiores terão razão de 0,4, já que os membros inferiores em conjuntos com os superiores formam o corpo humano. Dessa forma:

$\large v_{tronco}=\frac{\Delta S_{tronco}}{\Delta t_{dedo\ ao\ cerebro}-\Delta t_{pes\ ao\ tronco}}=\frac{1,7\cdot0,4}{30\cdot{10}^{-3}-20\cdot{10}^{-3}}$

$\large v_{tronco}=\frac{0,68}{10\cdot{10}^{-3}}=0,068\cdot{10}^3=68\ m/s$

Gabarito: D

Questão 73da prova de Física FUVEST 2020

A velocidade de escape de um corpo celeste é a mínima velocidade que um objeto deve ter nas proximidades da superfície desse corpo para escapar de sua atração gravitacional. Com base nessa informação e em seus conhecimentos sobre a interpretação cinética da temperatura, considere as seguintes afirmações a respeito da relação entre a velocidade de escape e a atmosfera de um corpo celeste.

I. Corpos celestes com mesma velocidade de escape retêm atmosferas igualmente densas, independentemente da temperatura de cada corpo.

II. Moléculas de gás nitrogênio escapam da atmosfera de um corpo celeste mais facilmente do que moléculas de gás hidrogênio.

III. Comparando corpos celestes com temperaturas médias iguais, aquele com a maior velocidade de escape tende a reter uma atmosfera mais densa.

Apenas é correto o que se afirma em

(A) I.

(B) II.

(D) I e II.

(E) I e III.

Resolução Comentada

Por definição, no infinito a energia potencial gravitacional é nula. Na situação de escape, a energia cinética do corpo a ser ejetado também tende a zero, quando ele chega no infinito. Isso nos permite escrever que:

$\large Epot+Ec=0$

$\large \frac{-G\cdot M_{planeta}\cdot m_{corpo}}{R_{planeta}}+\frac{m_{corpo}\cdot\left(v_{escape}\right)^2}{2}=0$

$\large \frac{-G\cdot M_{planeta}\cdot \cancel{m_{corpo}}}{R_{planeta}}+\frac{\cancel{m_{corpo}}\cdot\left(v_{escape}\right)^2}{2}=0$

$\large \frac{-G\cdot M_{planeta}}{R_{planeta}}+\frac{\left(v_{escape}\right)^2}{2}=0$

$\large \frac{\left(v_{escape}\right)^2}{2}=\frac{G\cdot M_{planeta}}{R_{planeta}}$

Afirmação I: Incorreta. Uma mesma relação de escape implica uma mesma razão entre a massa e o raio do planeta, considerando que o corpo a ser ejetado parte da sua superfície. A densidade é dada pela razão entre a massa e o volume do corpo. Ao aproximarmos o planeta a uma esfera, teremos que o seu volume se relaciona com o cubo de seu raio, tornando a afirmação incorreta.

Afirmação II: Incorreta. A velocidade média das moléculas de um gás é inversamente proporcional à raiz quadrada de sua massa molar. Dessa forma, quanto menor a massa molar, maior a velocidade média das partículas. A molécula de Hidrogênio, a uma mesma temperatura, deverá apresentar velocidade média maior que as de Nitrogênio.

Dessa forma, as moléculas de Hidrogênio tendem a atingir a velocidade de escape do planeta mais facilmente que as moléculas de Nitrogênio.

Afirmação III: Correta. A velocidade de escape é proporcional à massa do planeta. A uma mesma temperatura, adotando que os raios dos planetas sejam próximos, uma maior velocidade de escape implicará uma maior massa.

Se a densidade é dada pela razão entre massa e volume, uma maior velocidade de escape tende a implicar também uma maior densidade.

Gabarito: “C”

Questão 74

Um equipamento de bungee jumping está sendo projetado para ser utilizado em um viaduto de 30 m de altura. O elástico utilizado tem comprimento relaxado de 10 m. Qual deve ser o mínimo valor da constante elástica desse elástico para que ele possa ser utilizado com segurança no salto por uma pessoa cuja massa, somada à do equipamento de proteção a ela conectado, seja de 120 kg?

(A) 30 N/m

(B) 80 N/m

(D) 160 N/m

(E) 180 N/m

Note e adote:
Despreze a massa do elástico, as forças dissipativas e as dimensões da pessoa;
Aceleração da gravidade = 10m/s²

Resolução Comentada

Vamos adotar o nível de referência no solo abaixo do viaduto. Para a mínima constante elástica, o praticamente tenderá a encostar a ponta de seu cabelo nesse nível de referência. Pela conservação da energia mecânica, podemos escrever:

$\large E_{pot}=E_{el}$

$\large m\cdot g\cdot h=\frac{k\cdot x^2}{2}$

Note que a distensão da mola será a própria altura do viaduto subtraída do comprimento natural da corda, L₀

$\large m\cdot g\cdot h=\frac{k\cdot\left(h-L_0\right)^2}{2}$

$\large k=\frac{2\cdot m\cdot g\cdot h}{\left(h-L_0\right)^2}=\frac{2\cdot120\cdot10\cdot30}{\left(30-10\right)^2}=\frac{2\cdot120\cdot10\cdot30}{20\cdot20}$

$\large k=\frac{\cancel 2\cdot \cancel {120}\cdot \cancel {10}\cdot 30}{\cancel {20}\cdot \cancel {20}}=\frac{6\cdot 30}{1}=180\ N/m$

Gabarito: E

Questão 75da prova de Física FUVEST 2020

Um fabricante projetou resistores para utilizar em uma lâmpada de resistência L. Cada um deles deveria ter resistência R. Após a fabricação, ele notou que alguns deles foram projetados erroneamente, de forma que cada um deles possui uma resistência R_D = R/2. Tendo em vista que a que a lâmpada queimará se for percorrida por uma corrente elétrica superior a V / (R+L), em qual(is) dos circuitos a lâmpada queimará?

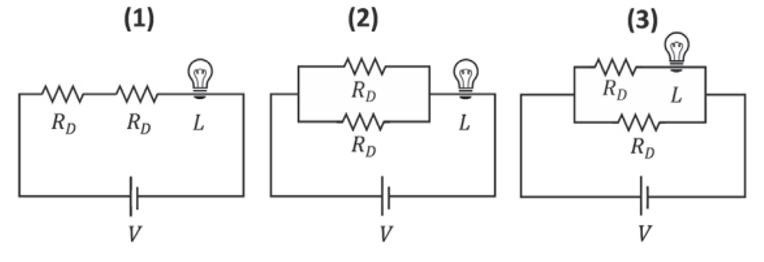
(A) 1, apenas.

(B) 2, apenas.

(D) 2 e 3, apenas.

(E) 1, 2 e 3.

Resolução Comentada

Na primeira situação, pela primeira lei de Ohm, temos:

$\large i_L=\frac{V}{Req_1}=\frac{V}{2\cdot R_D+L}=\frac{V}{2\cdot\frac{R}{2}+L}=\frac{V}{R+L}$

Se a corrente é superior à corrente limite, a lâmpada se queima nessa situação. No último caso, temos que a diferença de potência no ramo superior e inferior é a mesma, já que os dois estão ligados em paralelo. Isso nos permite escrever que:

$\large i_L=\frac{V}{Req_{superior}}=\frac{V}{R_D+L}=\frac{V}{\frac{R}{2}+L}$

No último caso, a lâmpada também se queima, visto que a corrente é superior à limite.

Gabarito: “D”

Questão 76

No dia 10 de abril de 2019, a equipe do Event Horizon Telescope (EHT, “Telescópio Horizonte de Eventos”) divulgou a primeira imagem de um buraco negro, localizado no centro da galáxia M87, obtida por um conjunto de telescópios com diâmetro efetivo equivalente ao da Terra, de 12.700 km. Devido ao fenômeno físico da difração, instrumentos óticos possuem um limite de resolução angular, que corresponde à mínima separação angular entre dois objetos que podem ser identificados separadamente quando observados à distância. O gráfico mostra o limite de resolução de um telescópio, medido em radianos, como função do seu diâmetro, para ondas luminosas de comprimento de onda de 1,3 mm, igual ao daquelas captadas pelo EHT. Note a escala logarítmica dos eixos do gráfico.

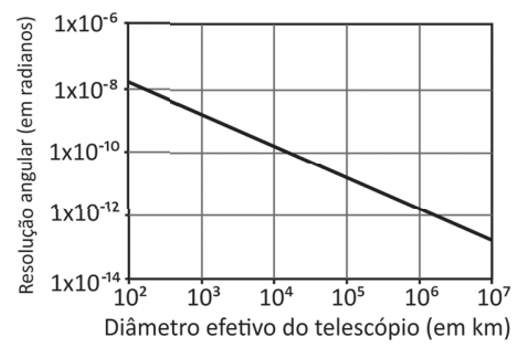
Sabe‐se que o tamanho equivalente a um pixel na foto do buraco negro corresponde ao valor da menor distância entre dois objetos naquela galáxia para que eles possam ser identificados separadamente pelo EHT. Com base nas informações anteriores e na análise do gráfico, e sabendo que a distância da Terra até a galáxia M87 é de 5 x 10²⁰km, indique o valor mais próximo do tamanho do pixel.

(A) 5 x 10¹ km

(B) 5 x 10⁴km

(D) 5 x 10¹⁰km

(E) 5 x 10¹³ km

Resolução Comentada

Devemos perceber o diâmetro efetivo do telescópio equivale ao da Terra, de 12.700 km:

$\large D_{efetivo}=12700\ km=1,27\cdot{10}^4\ km$

Pelo gráfico, somos capazes de determinar a resolução angular do telescópio:

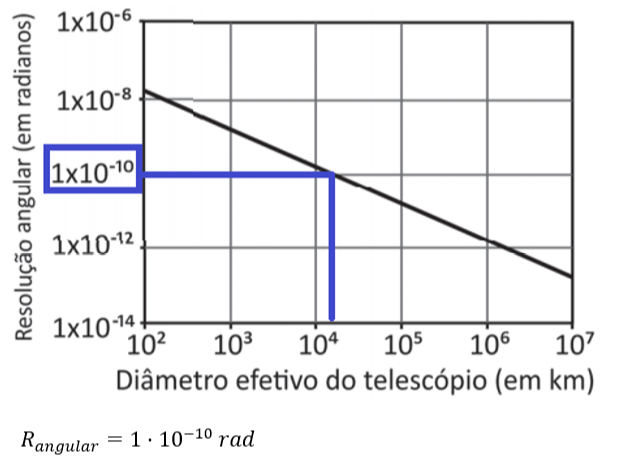
O tamanho do pixel pode ser aproximado ao tamanho do arco, fazendo a aproximação válida para pequenos ângulos:

$\large Arco=1\cdot{10}^{-10}\cdot5\cdot{10}^{20}=5\cdot{10}^{10}\ km$

Gabarito: “D”

Questão 77da prova de Física FUVEST 2020

Um solenoide muito longo é percorrido por uma corrente elétrica I,conforme mostra a figura 1.

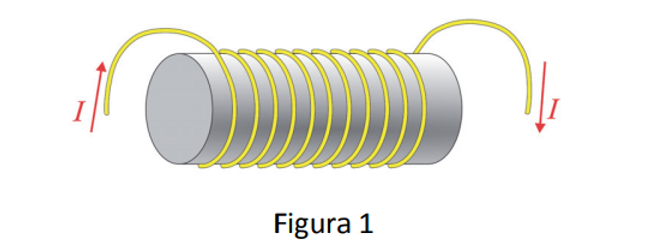
Em um determinado instante, uma partícula de carga q positiva desloca‐se com velocidade instantânea $\large \vec{v}$ perpendicular ao eixo do solenoide, na presença de um campo elétrico na direção do eixo do solenoide. A figura 2 ilustra essa situação, em uma seção reta definida por um plano que contém o eixo do solenoide.

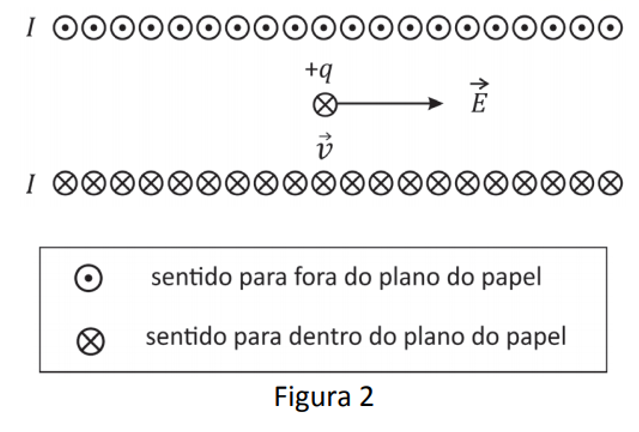
O diagrama que representa corretamente as forças elétrica $\large \vec{F}_{E}$ e magnética $\large \vec{F}_{B}$ , atuando sobre a partícula é:

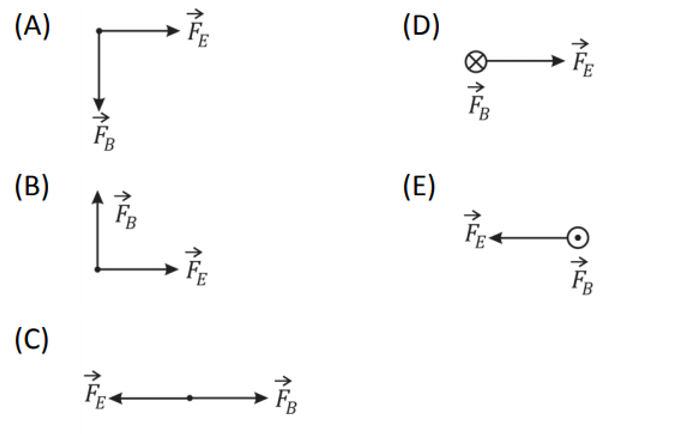
Resolução Comentada

Sendo o campo elétrico horizontal e com sentido da esquerda para a direita, temos que, para uma carga positiva, a força elétrica se orienta no mesmo sentido do campo, sendo também para a direita.

Se o solenoide é percorrido por uma corrente no sentido indicado na figura, somos capazes de determinar o sentido do campo magnético pela regra da mão direita envolvente:

Dessa forma, o campo magnético terá mesma direção e sentido que o campo elétrico. Usando a regra da mão esquerda espalmada, somos capazes de determinar a direção e sentido da força magnética:

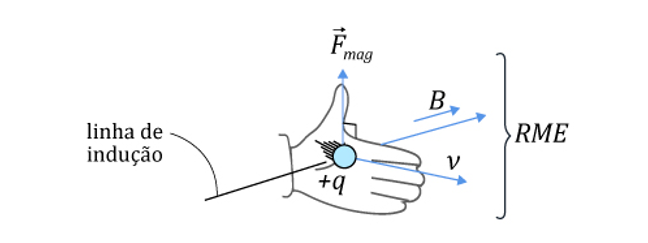
Para a velocidade entrando no plano do papel, e campo magnético horizontal e para a direita, temos força magnética vertical e para baixo, para uma carga positiva.

Gabarito: “A”.

Questão 78

Um drone voando na horizontal, em relação ao solo (como indicado pelo sentido da seta na figura), deixa cair um pacote de livros. A melhor descrição da trajetória realizada pelo pacote de livros, segundo um observador em repouso no solo, é dada pelo percurso descrito na

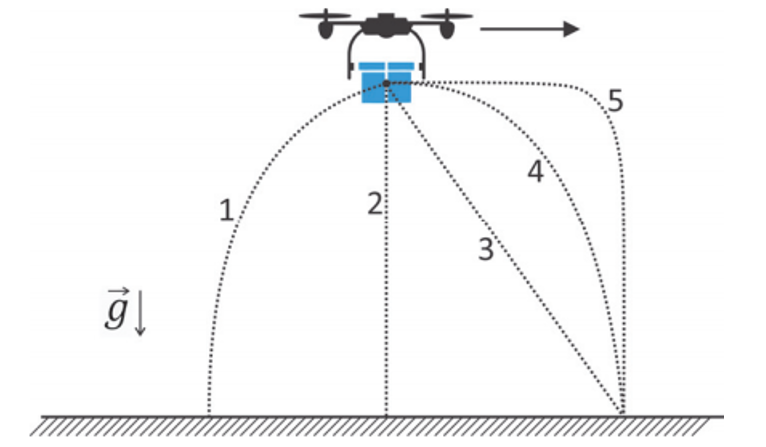
(A) trajetória 1.

(B) trajetória 2.

(D) trajetória 4.

(E) trajetória 5.

Resolução Comentada

Quando os livros são abandonados pelo drone, eles possuem velocidade horizontal inicial não nula e de mesmo módulo da velocidade horizontal do drone. A velocidade vertical inicial é nula, e possui aceleração positiva, de mesma orientação da gravidade.

Com isso, teremos a composição dos movimentos horizontal e vertical, formando uma trajetória parabólica representada na alternativa 4.

Gabarito: “D”.

Questão 79 da prova de Física FUVEST 2020

Um pêndulo simples é composto por uma haste metálica leve, presa a um eixo bem lubrificado, e por uma esfera pequena de massa muito maior que a da haste, presa à sua extremidade oposta. O período P para pequenas oscilações de um pêndulo é proporcional à raiz quadrada da razão entre o comprimento da haste metálica e a aceleração da gravidade local. Considere este pêndulo nas três situações:

Em um laboratório localizado ao nível do mar, na Antártida, a uma temperatura de 0° C.
No mesmo laboratório, mas agora a uma temperatura de 250 K.
Em um laboratório no qual a temperatura é de 32° F, em uma base lunar, cuja aceleração da gravidade é igual a um sexto daquela da Terra.

Indique a alternativa correta a respeito da comparação entre os períodos de oscilação P₁, P₂ e P₃ do pêndulo nas situações 1, 2 e 3, respectivamente.

(A) P₁ < P₂ < P₃

(B) P₁ = P₃ < P₂

(D) P₃ < P₂ < P₁

(E) P₁ < P₂ = P₃

Resolução Comentada

A FUVEST cobrou uma questão abordando o período de oscilação de um pêndulo simples em baixas oscilações em 2016. Na ocasião a relação não foi fornecida e o tema foi amplamente abordado na aula relacionada às forças do curso de Física do Estratégia Vestibulares.

O período de oscilação, P, de um pêndulo simples em ângulos pequenos (geralmente inferiores a 15°) pode ser calculado por:

$\large P=2\cdot\pi\sqrt{\frac{L}{g}}$

Período de oscilação de um pêndulo simples quando em baixas amplitudes.

$\large [P]=s$

$\large [L]=m$

$\large [g]=m/s^{2}$

Na qual L é o comprimento do fio e g é a aceleração da gravidade.

Vamos tomar a situação do laboratório da primeira alternativa como nossa referência. No caso do segundo laboratório, a temperatura é menor, já que 0 °C = 273 K. Uma menor temperatura implica um menor comprimento da haste, já que ela sofrerá diminuição do seu comprimento em função da diminuição de temperatura. Como consequência o período de oscilação na situação 2 é menor que na situação 1:

$\large P_{2}<p_{1}$

Para o laboratório 3, teremos o mesmo comprimento da haste que o laboratório 1, já que $\large 32\degree F=0\degree C=273K$ . Se a aceleração da gravidade lunar é menor que a terrestre, teremos que o período de oscilação será maior, como consequência:

$\large P_2<p_1<p_3$

Gabarito: “C”.

Conte comigo em sua caminhada, e para ficar sabendo de todas as notícias relativas aos mais diversos vestibulares ocorrendo em nosso país, convido você a seguir as mídias sociais do Estratégia Vestibulares. Sinta-se também convidado a seguir o meu perfil pessoal, no qual trarei questões resolvidas e mais dicas para sua preparação.

Resolução Comentada da prova de Física FUVEST 2020

Inscreva-se em nossa newsletter🦉

Prova de Física FUVEST 2020

Questão 69

Resolução Comentada

Questão 70da prova de Física FUVEST 2020

Resolução Comentada

Questão 71

Resolução Comentada

Questão 72

Resolução Comentada

Questão 73da prova de Física FUVEST 2020

Resolução Comentada

Questão 74

Resolução Comentada

Questão 75da prova de Física FUVEST 2020

Resolução Comentada

Questão 76

Resolução Comentada

Questão 77da prova de Física FUVEST 2020

Resolução Comentada

Questão 78

Resolução Comentada

Questão 79 da prova de Física FUVEST 2020

Resolução Comentada

Veja também:

Raquel Oshio

Resolução Comentada Prova de Química Fuvest 2020

Prova FUVEST 2020 – Geografia – Resolução Comentada

Dinâmica: definição, forças e Leis de Newton

Leis de Kepler: quais são, conceitos e fórmulas

Queda livre: o que é, fórmulas e questões de vestibulares

Resolução Comentada da prova de Física FUVEST 2020

Inscreva-se em nossa newsletter🦉

Prova de Física FUVEST 2020

Questão 69

Resolução Comentada

Questão 70da prova de Física FUVEST 2020

Resolução Comentada

Questão 71

Resolução Comentada

Questão 72

Resolução Comentada

Questão 73da prova de Física FUVEST 2020

Resolução Comentada

Questão 74

Resolução Comentada

Questão 75da prova de Física FUVEST 2020

Resolução Comentada

Questão 76

Resolução Comentada

Questão 77da prova de Física FUVEST 2020

Resolução Comentada

Questão 78

Resolução Comentada

Questão 79 da prova de Física FUVEST 2020

Resolução Comentada

Veja também:

Raquel Oshio

Resolução Comentada Prova de Química Fuvest 2020

Prova FUVEST 2020 – Geografia – Resolução Comentada

Você pode gostar também