Fala, pessoal. Tudo certo? Sou o prof. Lucas Costa, professor de Física do Estratégia Vestibulares. Escrevo este artigo para, juntos, resolvermos as questões de Física da prova da 2ª Fase do Vestibular da UNESP 2020. Vamos nessa?
2ª Fase UNESP 2020 – Física
Questão 19
Para montar a fachada de seu restaurante, o proprietário considera duas maneiras diferentes de prender uma placa na entrada, conforme as figuras 1 e 2. Nas duas maneiras, uma mesma placa de 4 m de comprimento e massa de 30 kg será presa a uma haste rígida de massa desprezível e de 6 m de comprimento, que será mantida em equilíbrio, na posição horizontal. Na situação da figura 1, a haste é presa a uma parede vertical por uma articulação A, de dimensões desprezíveis, e por um fio ideal vertical, fixo em uma marquise horizontal, no ponto B. Na situação da figura 2, a haste é presa à parede vertical pela mesma articulação A e por um fio ideal, preso no ponto C dessa parede.
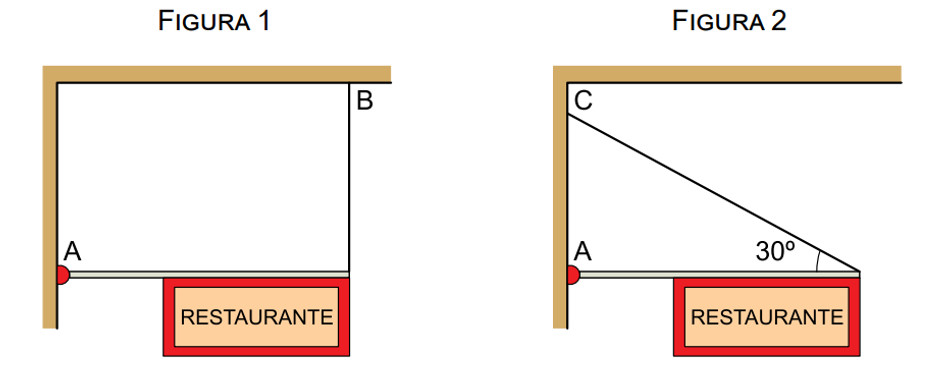
Considerando g= 10 m/s2
a) represente as forças que atuam na haste e calcule a intensidade, em N, da força de tração no fio que prende a haste à marquise, na situação da figura 1.
b) calcule a intensidade, em N, da força aplicada pela articulação sobre a haste, na situação da figura 2.
Gabarito
a) Devemos tomar cuidado, pois as forças que atuam na haste são a reação vertical no ponto A, a força normal de mesmo módulo, mesma direção e sentido oposto ao peso da placa e a força de tração proveniente do fio.
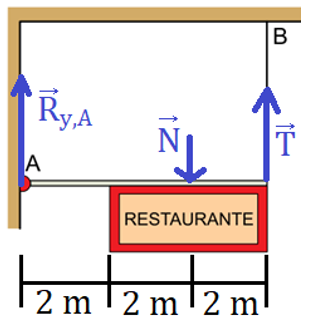
Podemos calcular o módulo da tração posicionando um apoio no ponto A. Perceba que o momento resultante nesse ponto deve nulo, já que o conjunto se encontra em equilíbrio:
A normal tem mesmo módulo do peso da placa, que será de e as distâncias são fornecidas pela figura acima:
A questão termina aqui, como aprofundamento, lembre-se que podemos calcular a sabendo que o somatório das forças verticais deve ser nulo:
b) Na situação da figura 2, temos as seguintes forças:
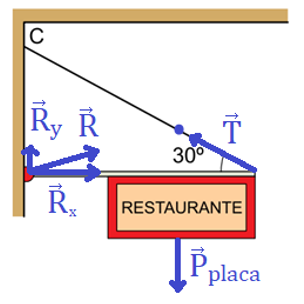
Novamente, podemos calcular o módulo da tração posicionando um apoio no ponto A. Perceba que o momento resultante nesse ponto deve nulo, já que o conjunto se encontra em equilíbrio:
Pelo equilíbrio das forças, temos:
Finalmente, o módulo da força resultante será dada pela soma vetorial:
Gabarito
a)
b)
Questão 20
Uma placa retangular de espessura desprezível e de vértices PQRS é posicionada, em repouso, sobre o eixo principal de um espelho esférico gaussiano de vértice V, foco principal F e centro de curvatura C, de modo que a posição do vértice R da placa coincida com a posição do ponto C, conforme figura. O raio de curvatura desse espelho mede 160 cm e o comprimento da placa é 40 cm.
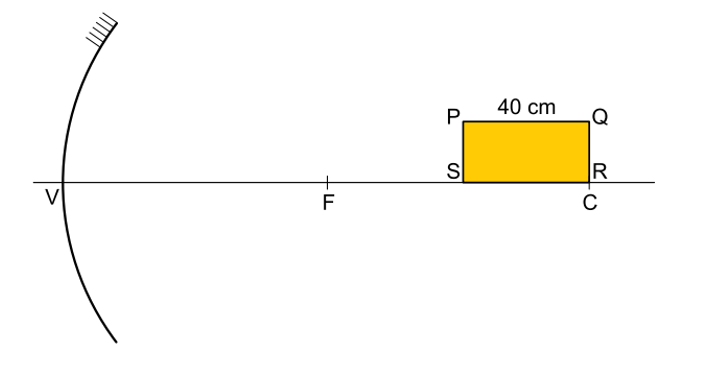
a) Na figura apresentada no campo de Resolução e Resposta, construa, traçando raios de luz, a imagem P’S’ do lado OS dessa placa. Identifique, nessa figura, os pontos P’ e S’ e classifique essa imagem como real ou virtual, justificando sua resposta.
b) Calcule, em cm, a distância entre a imagem P’S’, do lado PS, e a imagem Q’R’, do lado QR.
Gabarito
a) Se o raio de curvatura do espelho mede 160 cm, sabemos que a sua distância focal é de 80 cm. Se o comprimento da placa é de 40 cm notamos que o ponto S está 160-40=120 cm do vértice do espelho. Podemos calcular a distância do ponto S’ da imagem formada ao espelho usando a equação de Gauss:
Além disso, podemos calcular o aumento linear em função do foco e da distância p, entre o ponto S e o vértice do espelho:
Deduzimos que a imagem formado deverá ser invertida e maior. De fato, no centro de curvatura do espelho, formamos uma imagem invertida e mesmo tamanho do objeto, imagem essa que vai aumentando de tamanho até chegar até P’:
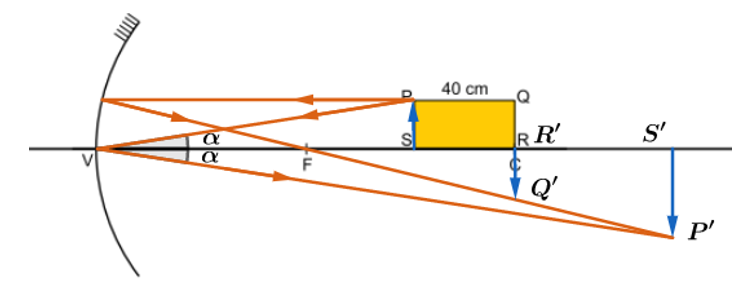
Devemos classificar a imagem como real e invertida.
b) Podemos perceber que a distância do ponto S’ até o vértice é de 240 cm e do centro até o vértice de 160 cm, daí:
Gabarito
a) Vide figura, imagem real e invertida.
b) d = 80 cm
Questão 21
O Programa Brasileiro de Etiquetagem (PBE) tem o objetivo de orientar o consumidor quanto ao consumo e à eficiência energética dos principais eletrodomésticos nacionais. A figura 1 ilustra a etiqueta de um chuveiro elétrico, apresentando a tensão nominal de funcionamento e as potências nominal e econômica (potência máxima e mínima do chuveiro). Em um banheiro, foram instalados esse chuveiro (C) e duas lâmpadas idênticas (L), de valores nominais (110\ V\ – 60 W) cada, conforme a figura 2.
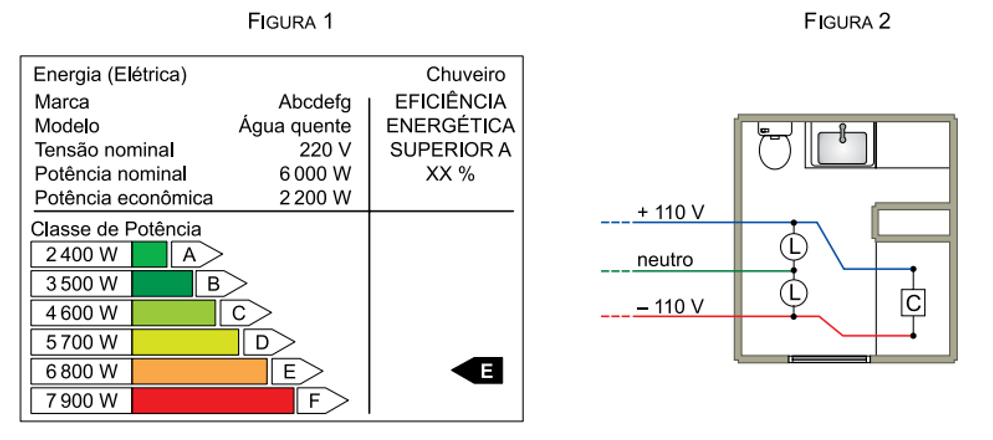
a) Calcule a intensidade da corrente elétrica, em ampères, que atravessa o chuveiro e determine a resistência elétrica, em , desse chuveiro quando ele opera com sua potência econômica.
b) Considere que as duas lâmpadas desse banheiro fiquem acesas simultaneamente por 30 minutos e que, nesse intervalo de tempo, o chuveiro permaneça ligado por 20 minutos, operando com sua potência nominal. Admitindo que 1 kWh de energia elétrica custe R$ 0,50, calcule o gasto, em reais, gerado nos 30 minutos desse banho, devido ao funcionamento do chuveiro e das lâmpadas.
Gabarito
a) Atenção aluno, mais um item da UNESP na qual são pedidas duas informações em uma mesma alternativa. Podemos começar calculando a corrente que atravessa a o chuveiro na operação com sua potência econômica:
Agora podemos determinar a sua resistência, fazendo uso de outra equação que relaciona a potência elétrica com a resistência do aparelho:
b) Podemos calcular a energia gasta pelos equipamentos multiplicando a sua potência, em , pelo tempo, em horas, durante o qual ficaram ligados:
Agora podemos calcular a energia total, e o gasto em reais do banho:
E o gasto, sabendo que cada kWh custa R$ 0,50:
Gabarito
a) e
b)
Com isso, encerramos a nossa correção de Física da 2ª Fase da UNESP 2020. Se ficou alguma dúvida, pode entrar em contato comigo através do nosso Fórum de Dúvidas ou pelas minhas redes sociais. Vou deitar esta correção disponível para download. Você vai poder baixar de forma gratuita no link a seguir.
Abraços
Prof. Lucas Costa
Instagram: @prof.lucascosta



